题目内容
 如图,在四棱柱ABCD-A1B1C1D1中,各条棱长都相等,AC=
如图,在四棱柱ABCD-A1B1C1D1中,各条棱长都相等,AC=| 3 |
考点:直线与平面垂直的判定
专题:平面向量及应用,空间位置关系与距离
分析:(1)由
2=(
+
+
)2,能求出BD1的棱长.
(2)过A1作A1O⊥平面ABCD,O为垂足.可证O在∠BAD的角平分线,即AC上,可得BD⊥AC,BD⊥A1O,从而可证BD⊥平面ACC1A1.
| BD1 |
| BA |
| AD |
| DD1 |
(2)过A1作A1O⊥平面ABCD,O为垂足.可证O在∠BAD的角平分线,即AC上,可得BD⊥AC,BD⊥A1O,从而可证BD⊥平面ACC1A1.
解答:
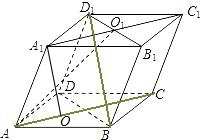 解:(1)∵在四棱柱ABCD-A1B1C1D1中,各条棱长都相等,AC=
解:(1)∵在四棱柱ABCD-A1B1C1D1中,各条棱长都相等,AC=
,∠BAD=60°,
∴可解得:平行六面体ABCD-A1B1C1D1的棱长均为1,
∠BAD=60°,∠BAA1=∠DAA1=45°,
∴
2=(
+
+
)2=
2+
2+
2+2|
||
|•cos60°+2|
||
|•cos135°+2|
||
|•cos45°
=1+1+1+1-
+
=4,
∴对角线BD1的长为2.
(2)解:过A1作A1O⊥平面ABCD,O为垂足.
∵∠BAA1=∠DAA1,AB=AD,各条棱长都相等,
∴O在∠BAD的角平分线,即AC上,
∴BD⊥AC,BD⊥A1O,
∵AC∩A1O=O,A1C1∥AC,C1?平面ACA1C1,
∴BD⊥平面ACC1A1.
 解:(1)∵在四棱柱ABCD-A1B1C1D1中,各条棱长都相等,AC=
解:(1)∵在四棱柱ABCD-A1B1C1D1中,各条棱长都相等,AC=| 3 |
∴可解得:平行六面体ABCD-A1B1C1D1的棱长均为1,
∠BAD=60°,∠BAA1=∠DAA1=45°,
∴
| BD1 |
| BA |
| AD |
| DD1 |
| BA |
| AD |
| DD1 |
| BA |
| AD |
| AD |
| DD1 |
| BA |
| DD1 |
=1+1+1+1-
| 2 |
| 2 |
∴对角线BD1的长为2.
(2)解:过A1作A1O⊥平面ABCD,O为垂足.
∵∠BAA1=∠DAA1,AB=AD,各条棱长都相等,
∴O在∠BAD的角平分线,即AC上,
∴BD⊥AC,BD⊥A1O,
∵AC∩A1O=O,A1C1∥AC,C1?平面ACA1C1,
∴BD⊥平面ACC1A1.
点评:本题考查对角线的长的求法,直线与平面垂直的判定,解题时要认真审题,注意向量法的合理运用,属于基本知识的考查.

练习册系列答案
相关题目
设曲线y=ax3在点(1,a)处的切线与直线6x-y+2=0平行,则a=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、非充非要条件 |
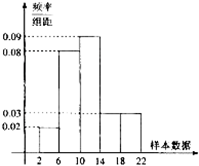 样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的
样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的