题目内容
11.已知函数f(x)=|2x-1|+x+$\frac{1}{2}$的最小值为m.(1)求m的值;
(2)若a,b,c是正实数,且a+b+c=m,求证:2(a2+b2+c2)≥ab+bc+ca-3abc.
分析 (1)写出分段函数,即可求m的值;
(2)利用作差法,即可证明.
解答 (1)解:$f(x)=|{2x-1}|+x+\frac{1}{2}=\left\{{\begin{array}{l}{3x-\frac{1}{2},x≥\frac{1}{2}}\\{-x+\frac{3}{2},x<\frac{1}{2}}\end{array}}\right.$,
所以$f{(x)_{min}}=f({\frac{1}{2}})=1$,即m=1.
(2)证明:由于a3+b3-a2b-ab2=(a2-b2)(a-b)=(a-b)2(a+b)≥0,
由于a+b+c=1,所以a3+b3≥a2b+ab2=ab(a+b)=ab(1-c)=ab-abc,
同理可证:b3+c3≥bc-abc,c3+a3≥ca-abc,
三式相加得2(a3+b3+c3)≥ab+bc+ca-3abc.
点评 本题考查分段函数,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
6.若直线l∥平面α,直线a?平面α,则l与a( )
| A. | 平行 | B. | 异面 | C. | 相交 | D. | 没有公共点 |
16.下列关于幂函数y=xα(α∈Q)的论述中,正确的是( )
| A. | 当α=0时,幂函数的图象是一条直线 | |
| B. | 幂函数的图象都经过(0,0)和(1,1)两个点 | |
| C. | 若函数f(x)为奇函数,则f(x)在定义域内是增函数 | |
| D. | 幂函数f(x)的图象不可能在第四象限内 |
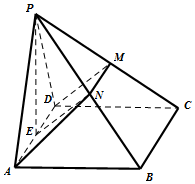 在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.
在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.