题目内容
(12分)已知定义域为 的偶函数
的偶函数 .
.
(1)求实数 的值;
的值;
(2)判断并证明 的单调性;
的单调性;
(3)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ;
;
(2)设 ,则
,则

当 时,
时, 为
为 上的增函数;当
上的增函数;当 时,
时, 为
为 上的减函数。(3)
上的减函数。(3) 。
。
解析试题分析:(1)
 …… ……………………………………………3分
…… ……………………………………………3分
⑵设
则



当 时,
时, ,
, ,
, 为
为 上的增函数;
上的增函数;
当 时,
时, ,
, ,
, 为
为 上的增函数。
上的增函数。
综上可得,当 时,
时, 为
为 上的增函数。
上的增函数。
同理可证,当 时,
时, 为
为 上的减函数。 ………………7分
上的减函数。 ………………7分
⑶ 对任意
对任意 恒成立,
恒成立, 对任意
对任意 恒成立,
恒成立, 对任意
对任意 恒成立,
恒成立, 对任意
对任意 恒成立
恒成立 对任意
对任意 恒成立,(令
恒成立,(令 )
) ……………………………………12分
……………………………………12分
考点:函数的奇偶性;函数的单调性;函数性质的综合应用。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
. 解集.
解集. 。
。 ,求a的值;
,求a的值; 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m) 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。 上的奇函数
上的奇函数 (
( 、
、 )过已知点
)过已知点 .
. 在区间
在区间 是增函数;若函数
是增函数;若函数 在区间
在区间 (其中
(其中 )也是增函数,求
)也是增函数,求 的最小值;
的最小值; 的解集.
的解集. .
.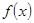 在
在 上为增函数;
上为增函数; 的值;
的值; 上的值域.
上的值域. <ln(x+1)<x;
<ln(x+1)<x;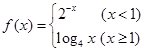 ,
,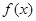 的图像;
的图像;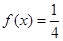 的
的 的取值.
的取值.
 的定义域;
的定义域; ,求
,求 的值.
的值. 的一系列对应值如下表:
的一系列对应值如下表:










 的解析式;
的解析式; 周期为
周期为 ,求
,求 在区间
在区间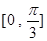 上的最大、最小值及对应的
上的最大、最小值及对应的