题目内容
已知x+2y+3z=2,则x2+y2+z2的最小值是 .
考点:二维形式的柯西不等式
专题:不等式的解法及应用
分析:由条件利用柯西不等式(12+22+32)(x2+y2+z2)≥(x+2y+3z)2,求得x2+y2+z2的最小值.
解答:
解:12+22+32=14,∴由柯西不等式可得(12+22+32)(x2+y2+z2)≥(x+2y+3z)2=4,
∴x2+y2+z2≥
=
,即x2+y2+z2的最小值是
,
故答案为:
.
∴x2+y2+z2≥
| 4 |
| 14 |
| 2 |
| 7 |
| 2 |
| 7 |
故答案为:
| 2 |
| 7 |
点评:本题主要考查了函数的最值,以及柯西不等式的应用,解题的关键是利用柯西不等式(12+22+32)(x2+y2+z2)≥(x+2y+3z)2,进行解决.

练习册系列答案
相关题目
复数
的共轭复数对应的点位于( )
| 1-i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合P={x|x≥0},Q={x|
≥0},则P∩(∁RQ)=( )
| x+1 |
| x-2 |
| A、(-∞,1) |
| B、(-∞,1] |
| C、(-1,0) |
| D、[0,2] |
在正八边形的8个顶点中,任取4个点,则以这4个点为顶点的四边形是梯形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=f(x)的定义域为{x|x∈R,且x≠2},且y=f(x+2)是偶函数,当x<2时,f(x)=|2x-1|,那么当x>2时,函数f(x)的递减区间是( )
| A、(3,5) |
| B、(3,+∞) |
| C、(2,+∞) |
| D、(2,4] |
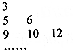 设{an}是集合{2s+2t|0≤s<t,且s、t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}中的各项按照上小下大、左小右大的原则写成如图所示的三角形数阵,则a99=
设{an}是集合{2s+2t|0≤s<t,且s、t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}中的各项按照上小下大、左小右大的原则写成如图所示的三角形数阵,则a99=