题目内容
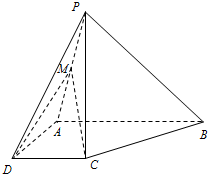 如图,在四棱锥P-ABCD中,AD=CD=
如图,在四棱锥P-ABCD中,AD=CD=| 1 |
| 2 |
(1)求证:BC⊥平面PAC;
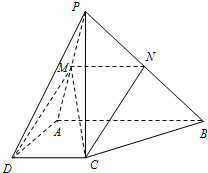
(2)若M为线段PA的中点,且过C,D,M三点的平面与PB交于点N,求PN:PB的值.
考点:直线与平面垂直的判定,余弦定理
专题:综合题,空间位置关系与距离
分析:(1)连结AC,证明BC⊥AC,BC⊥PC,利用线面垂直的判定定理,可得BC⊥平面PAC;
(2)证明AB∥MN,利用M为线段PA的中点,可得N为线段PB的中点,即可得出结论.
(2)证明AB∥MN,利用M为线段PA的中点,可得N为线段PB的中点,即可得出结论.
解答:
 (1)证明:连结AC.不妨设AD=1.
(1)证明:连结AC.不妨设AD=1.
因为AD=CD=
AB,所以CD=1,AB=2.
因为∠ADC=90°,所以AC=
,∠CAB=45°.
在△ABC中,由余弦定理得BC=
,所以AC2+BC2=AB2.
所以BC⊥AC. …(3分)
因为PC⊥平面ABCD,BC?平面ABCD,所以BC⊥PC. …(5分)
因为PC?平面PAC,AC?平面PAC,PC∩AC=C,
所以BC⊥平面PAC. …(7分)
(2)解:如图,因为AB∥DC,CD?平面CDMN,AB?平面CDMN,
所以AB∥平面CDMN. …(9分)
因为AB?平面PAB,
平面PAB∩平面CDMN=MN,
所以AB∥MN. …(12分)
在△PAB中,因为M为线段PA的中点,
所以N为线段PB的中点,
即PN:PB的值为
. …(14分)
 (1)证明:连结AC.不妨设AD=1.
(1)证明:连结AC.不妨设AD=1.因为AD=CD=
| 1 |
| 2 |
因为∠ADC=90°,所以AC=
| 2 |
在△ABC中,由余弦定理得BC=
| 2 |
所以BC⊥AC. …(3分)
因为PC⊥平面ABCD,BC?平面ABCD,所以BC⊥PC. …(5分)
因为PC?平面PAC,AC?平面PAC,PC∩AC=C,
所以BC⊥平面PAC. …(7分)
(2)解:如图,因为AB∥DC,CD?平面CDMN,AB?平面CDMN,
所以AB∥平面CDMN. …(9分)
因为AB?平面PAB,
平面PAB∩平面CDMN=MN,
所以AB∥MN. …(12分)
在△PAB中,因为M为线段PA的中点,
所以N为线段PB的中点,
即PN:PB的值为
| 1 |
| 2 |
点评:本题考查线面平行、垂直的判定,考查学生分析解决问题的能力,正确运用线面平行、垂直的判定定理是关键.

练习册系列答案
相关题目
“x<1”是“log2(x+1)<1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=
+
的定义域是( )
| sinx |
| -cosx |
A、[kπ+
| ||
B、[kπ+
| ||
C、[2kπ+
| ||
| D、[2kπ,(2k+1)π](k∈Z) |