题目内容
F是双曲线C:
-
=1(a>0,b>0)的右焦点,过点F向C的一条渐近线引垂线,垂足为A,交另一条渐近线于点B.若2
=
,则C的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:双曲线的简单性质
专题:平面向量及应用,圆锥曲线的定义、性质与方程
分析:设一渐近线OA的方程为y=
x,设A(m,
m),B(n,-
),由 2
=
,求得点A的坐标,再由FA⊥OA,斜率之积等于-1,求出a2=3b2,代入e=
=
进行运算.
| b |
| a |
| b |
| a |
| bn |
| a |
| AF |
| FB |
| c |
| a |
| ||
| a |
解答:
解:由题意得右焦点F(c,0),设一渐近线OA的方程为y=
x,
则另一渐近线OB的方程为 y=-
x,
设A(m,
),B(n,-
),
∵2
=
,
∴2(c-m,-
)=(n-c,-
),
∴2(c-m)=n-c,-
=-
,
∴m=
c,n=
,
∴A(
,
).
由FA⊥OA可得,斜率之积等于-1,
即
•
=-1,
∴a2=3b2,∴e=
=
=
.
故选:A.
| b |
| a |
则另一渐近线OB的方程为 y=-
| b |
| a |
设A(m,
| bm |
| a |
| bn |
| a |
∵2
| AF |
| FB |
∴2(c-m,-
| bm |
| a |
| bn |
| a |
∴2(c-m)=n-c,-
| 2bm |
| a |
| bn |
| a |
∴m=
| 3 |
| 4 |
| 3c |
| 2 |
∴A(
| 3c |
| 4 |
| 3bc |
| 4a |
由FA⊥OA可得,斜率之积等于-1,
即
| ||
|
| b |
| a |
∴a2=3b2,∴e=
| c |
| a |
| ||
| a |
2
| ||
| 3 |
故选:A.
点评:本题主要考查双曲线的标准方程,以及双曲线的简单性质的应用,同时考查向量的共线的坐标表示,求得点A的坐标是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若变量x,y满足约束条件
,则x-2y最小值为( )
|
| A、0 | ||
B、
| ||
| C、-1 | ||
| D、4 |
已知i是虚数单位,若复数z满足(z-i)(3-i)=10,则复数z所对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
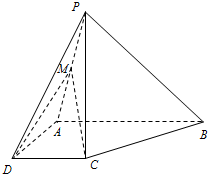 如图,在四棱锥P-ABCD中,AD=CD=
如图,在四棱锥P-ABCD中,AD=CD=