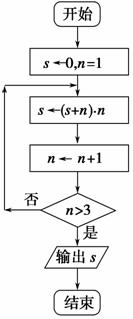
题目内容
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1) 求数列{bn}的通项公式bn;
(2) 设数列{an}的通项an=loga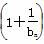 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与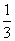 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
解:(1) 设数列{bn}的公差为d,
由题意得
∴ bn=3n-2.
(2) 由bn=3n-2,知

而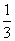 logabn+1=loga
logabn+1=loga ,于是,比较Sn与
,于是,比较Sn与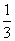 logabn+1的大小
logabn+1的大小
比较 的大小 .
的大小 .
 ① 当n=1时,已验证(*)式成立;
① 当n=1时,已验证(*)式成立;
② 假设n=k(k≥1)时(*)式成立,即
则当n=k+1时,
 从而(1+1)
从而(1+1)  即当n=k+1时,(*)式成立.由①②知(*)式对任意正整数n都成立.于是,当a>1时,Sn>
即当n=k+1时,(*)式成立.由①②知(*)式对任意正整数n都成立.于是,当a>1时,Sn>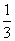 logabn+1,当 0<a<1时,Sn<
logabn+1,当 0<a<1时,Sn<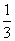 logabn+1.
logabn+1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
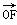 ·
· =1.设|
=1.设|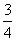 c.若以O为中心,F为一个焦点的椭圆经过点Q,当
c.若以O为中心,F为一个焦点的椭圆经过点Q,当 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.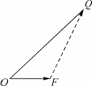
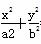 =1(a>b>0)外,过P0作椭圆的两条切线的切点分别为P1、P2,则切点弦P1P2所在的直线方程是
=1(a>b>0)外,过P0作椭圆的两条切线的切点分别为P1、P2,则切点弦P1P2所在的直线方程是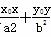 =1.那么对于双曲线则有如下命题:若P0(x0,y0)在双曲线
=1.那么对于双曲线则有如下命题:若P0(x0,y0)在双曲线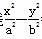 =1(a>0,b>0)外,过P0作双曲线的两条切线的切点分别为P1、P2,则切点弦P1P2所在的直线方程是________.
=1(a>0,b>0)外,过P0作双曲线的两条切线的切点分别为P1、P2,则切点弦P1P2所在的直线方程是________.

 ,
, ”的否定是( )
”的否定是( ) ,
,
 ,
, 和平面
和平面 ,则
,则 的一个必要条件是
的一个必要条件是 ,
, (B)
(B) ,
,
 (D)
(D)