题目内容
4.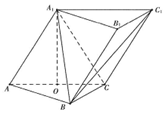 在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求三棱锥C1-ABC的体积.
分析 (Ⅰ)推导出A1O⊥AC,由此能证明A1O⊥平面ABC.
(Ⅱ)推导出C1到平面ABC的距离等于A1到平面ABC的距离,从而${V_{{C_1}-ABC}}={V_{{A_1}-ABC}}$,由此能求出三棱锥C1-ABC的体积.
解答 (本小题满分12分)
证明:(Ⅰ)∵AA1=A1C,且O为AC的中点,
∴A1O⊥AC,…(2分)
又∵平面AA1C1C⊥平面ABC,
平面AA1C1C∩平面ABC=AC…(4分)
且A1O?平面AA1C1C,
∴A1O⊥平面ABC…(6分)
解:(Ⅱ)∵A1C1∥AC,A1C1?平面ABC,AC?平面ABC,
∴A1C1∥平面ABC,
即C1到平面ABC的距离等于A1到平面ABC的距离…(8分)
由(Ⅰ)知A1O⊥平面ABC且${A_1}O=\sqrt{A{A_1}^2-A{O^2}}=\sqrt{3}$,…(9分)
∴三棱锥C1-ABC的体积:
${V_{{C_1}-ABC}}={V_{{A_1}-ABC}}=\frac{1}{3}{S_{△ABC}}•{A_1}O=\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\sqrt{3}=1$…(12分)
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
14.设i是虚数单位,复数i(1+ai)为纯虚数,则实数a为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
15.已知直线l:y=k(x+$\sqrt{3}$)和圆C:x2+(y-1)2=1,若直线l与圆C相切,则k=( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$或0 | D. | $\sqrt{3}$或0 |
12.抛物线x2=4y的焦点到准线的距离为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |