题目内容
锐角△ABC中,若C=2B,则
的范围是 .
| AB |
| AC |
考点:正弦定理
专题:解三角形
分析:由已知C=2B可得A=180°-3B,再由锐角△ABC可得B的范围,由正弦定理可得,
=
=2cosB.
| AB |
| AC |
| sinC |
| sinB |
解答:
解:因为锐角△ABC中,若C=2B所以A=180°-3B,
∴
,
∴30°<B<45°,
由正弦定理可得,
=
=2cosB,
∵
<cosB<
,
∴
<
<
,
故答案为:(
,
).
∴
|
∴30°<B<45°,
由正弦定理可得,
| AB |
| AC |
| sinC |
| sinB |
∵
| ||
| 2 |
| ||
| 2 |
∴
| 2 |
| AB |
| AC |
| 3 |
故答案为:(
| 2 |
| 3 |
点评:本题主要考查了三角形的内角和定理,正弦定理在解三角形的应用.属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,则f(f(2))=( )
|
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
根据如下样本数据:
得到的回归方程为
=
x+
,则( )
| X | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 2 | -1 | 1 | -2 | -3 |
 |
| y |
 |
| b |
 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若点P(-m,4)是角α终边上一点,且cosα=-
,则m的值为( )
| 3 |
| 5 |
| A、3 | B、-3 | C、±3 | D、5 |
设全集U=R,A={x||x-1|<1},B={x|y=
},则图中阴影部分表示的集合是( )
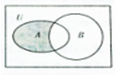
| 1 | ||
|

| A、{x|x≥1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1≤1} |