Question

8．已知函数f（x）对任意的x∈R都有f（x）+f（-x）=0，且当x＞0时，f（x）=ln（2x+1），则函数f（x）的大致图象为（　　）

• A．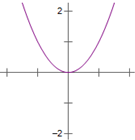
• B．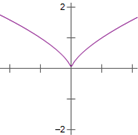
• C．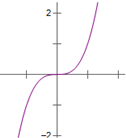
• D．

Answer 1

分析 根据f（x）的奇偶性和变化快慢可判断出图象．

解答 解：∵f（x）+f（-x）=0，
∴f（-x）=-f（x），
∴f（x）是奇函数，图象关于原点对称，排除A，B．
又∵当x＞0时，f（x）=ln（2x+1），
∴当x＞0时，f（x）的增长速度越来越慢，排除C．
故选：D．

点评 本题考查了函数的奇偶性及函数增长模型，是基础题．