题目内容
18．已知a∈（0，$\frac{π}{2}$），且2sin2α-sinαcosα-3cos2α=0，则$\frac{sin（α+\frac{π}{2}）}{sin2α+cos2α+1}$$\frac{\sqrt{13}}{10}$．分析 利用已知条件求出tanα的值，然后求解所求表达式的值．
解答 解：α∈（0，$\frac{π}{2}$），且2sin2α-sinαcosα-3cos2α=0，
所以2tan2α-tanα-3=0，解得tanα=$\frac{3}{2}$，tanα=-$\frac{1}{2}$（舍去）
cosα=$\sqrt{\frac{{cos}^{2}α}{{sin}^{2}α+{cos}^{2}α}}$=$\sqrt{\frac{1}{{tan}^{2}α+1}}$=$\sqrt{\frac{4}{13}}$，sinα=$\sqrt{1-\frac{4}{13}}$=$\frac{3}{\sqrt{13}}$
$\frac{sin（α+\frac{π}{2}）}{sin2α+cos2α+1}$=$\frac{cosα}{2sinαcosα+2{cos}^{2}α}$=$\frac{1}{2×\frac{3}{\sqrt{13}}+2×\frac{2}{\sqrt{13}}}$=$\frac{\sqrt{13}}{10}$．
故答案为：$\frac{\sqrt{13}}{10}$，
点评 本题考查三角函数的化简求值，同角三角函数的基本关系式的应用，考查计算能力．
练习册系列答案
小学课时特训系列答案
相关题目
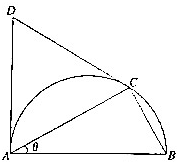如图是一个半径为1的半圆，AB是直径，点C在圆弧上，且与A、B不重合，△ACD是等边三角形，设∠CAB=θ（0＜θ＜$\frac{π}{2}$），