题目内容
已知函数f(x)=ax2+bx+1(a,b∈R),x∈R.
(1)若函数f(x)的最小值为f(-1)=0,求f(x)的解析式,并写出单调区间;
(2)在(1)的条件下,f(x)>x+k在区间[-3,-1]上恒成立,试求k的范围
解 (1)由题意有
f(-1)=a-b+1=0,且- =-1,∴a=1,b=2.
=-1,∴a=1,b=2.
∴f(x)=x2+2x+1,单调减区间为(-∞,-1],单调增区间为[-1,+∞)
(2)f(x)>x+k在区间[-3,-1]上恒成立,转化为x2+x+1>k在区间[-3,-1]上恒成立.
设g(x)=x2+x+1,x∈[-3,-1],则g(x)在[-3,-1]上递减.
∴g(x)min=g(-1)=1.
∴k<1,即k的取值范围为(-∞,1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若g(m)=0,则实数m的值等于( )
,若g(m)=0,则实数m的值等于( )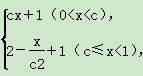 且满足f(c2)=
且满足f(c2)=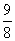 ,其中0<c<1.
,其中0<c<1.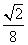 +1.
+1.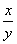 )=f(x)-f(y).
)=f(x)-f(y). )<2.
)<2.