题目内容
18.已知定义域为R的函数f(x)满足f(f(x)-x2+x)=f(x)-x2+x.(1)若f(3)=3,求f(-3)的值;
(2)若有且仅有一个实数x0满足f(x0)=x0’且函数$g(x)=\frac{1}{{{4^x}+m•{2^x}+4}}$的定义域为R,
①求实数m的取值范围;
②求f(m)的取值范围.
分析 (1)根据题意,由f(f(x)-x2+x)=f(x)-x2+x,将x=3代入,有f(f(3)-32+3)=f(3)-32+3=-3,整理可得f(-3)的值;
(2)①根据题意,由于函数$g(x)=\frac{1}{{{4^x}+m•{2^x}+4}}$的定义域为R,分析可得$-m≠{2^x}+\frac{4}{2^x},而易知{2^x}+\frac{4}{2^x}≥4$,由基本不等式的性质分析可得答案;
②根据题意,由于有且仅有一个实数x0满足f(x0)=x0成立,分析可得f(x)-x2+x=x0,分析可得f(x)的解析式,分析其解的情况,可得f(m)=m2-m+1,m∈(-4,+∞),由二次函数的性质分析可得答案.
解答 解:(1)因为f(f(x)-x2+x)=f(x)-x2+x,f(3)=3
所以f(f(3)-32+3)=f(3)-32+3,
又由f(3)=3,代入可得f(3-32+3)=-3,
所以f(-3)=-3,
(2)①因为函数$g(x)=\frac{1}{{{4^x}+m•{2^x}+4}}$的定义域为R,
所以4x+m•2x+4≠0对任意实数成立
所以$-m≠{2^x}+\frac{4}{2^x},而易知{2^x}+\frac{4}{2^x}≥4$
所以-m<4,所以m>-4
故m的取值范围是(-4,+∞),
②因为f(f(x)-x2+x)=f(x)-x2+x对x∈R恒成立
又因为有且仅有一个实数x0满足f(x0)=x0
所以对任意x∈R,有f(x)-x2+x=x0
令$x={x_0},则f({x_0})-{x_0}^2+{x_0}={x_0}$
所以由$f({x_0})={x_0}得{x_0}-{x_0}^2=0,故{x_0}=0,或{x_0}=1$,
所以f(x)-x2+x=0或f(x)-x2+x=1
所以f(x)=x2-x或f(x)=x2-x+1
而当f(x)=x2-x时,f(x)=x有两个解,舍去
当f(x)=x2-x+1时,f(x)=x只有一个解,
故f(x)=x2-x+1
所以f(m)=m2-m+1,m∈(-4,+∞)
所以f(m)的取值范围是$[{\frac{3}{4},+∞})$.
点评 本题考查函数的解析式、函数的值的计算,关键是理解函数的定义,能准确分析“有且仅有一个实数x0满足f(x0)=x0”的含义.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
| A. | [1,3) | B. | (1,3) | C. | (0,3] | D. | (-∞,-5]∪[6,+∞) |
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | $(-\frac{2}{e},2e)$ | D. | $[-\frac{3}{e},3e]$ |
| A. | $\frac{{\sqrt{13}}}{2}$ | B. | $\frac{3}{2}$ | C. | $1+\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
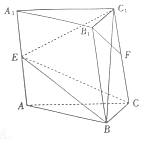 如图,已知直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1,CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1,CC1的中点,且BE⊥B1F.