题目内容
7.在平面直角坐标系xOy中,A点的直角坐标为$(\sqrt{3}+2cosα,1+2sinα)$(α为参数).在以原点O为极点,x轴正半轴为极轴的极坐标中,直线的极坐标方程为$2ρcos(θ+\frac{π}{6})=m$.(m为实数).(1)试求出动点A的轨迹方程(用普通方程表示)
(2)设A点对应的轨迹为曲线C,若曲线C上存在四个点到直线的距离为1,求实数m的取值范围.
分析 (1)由题意写出A的参数方程$\left\{\begin{array}{l}{x=\sqrt{3}+2cosα}\\{y=1+2sinα}\end{array}\right.$,把两式移项平方作和得答案;
(2)化直线的极坐标方程为直角坐标方程,画出图形,应用点到直线的距离公式求解.
解答 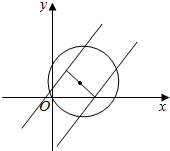 解:(1)设A(x,y),又A点的直角坐标为$(\sqrt{3}+2cosα,1+2sinα)$,
解:(1)设A(x,y),又A点的直角坐标为$(\sqrt{3}+2cosα,1+2sinα)$,
∴$\left\{\begin{array}{l}{x=\sqrt{3}+2cosα}\\{y=1+2sinα}\end{array}\right.$,把两式移项平方作和得:$(x-\sqrt{3})^{2}+(y-1)^{2}=4$;
(2)由$2ρcos(θ+\frac{π}{6})=m$,
得$2ρ×\frac{\sqrt{3}}{2}cosθ-2ρ×\frac{1}{2}sinθ=m$,即$\sqrt{3}x-y-m=0$,
如图,要使曲线C上存在四个点到直线的距离为1,
则圆C的圆心C($\sqrt{3},1$)到直线$\sqrt{3}x-y-m=0$的距离小于1.
即$\frac{|3-1-m|}{2}$<1,解得0<m<4.
点评 本题考查简单曲线的极坐标方程,考查了参数方程化普通方程,考查数形结合的解题思想方法,训练了点到直线的距离公式的应用,是中档题.

练习册系列答案
相关题目
18.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px的通径为4,则P=( )
| A. | 1 | B. | 4 | C. | 2 | D. | 8 |
16.已知U={1,2,3,4},集合A={1,4},则∁UA=( )
| A. | {2} | B. | {3} | C. | {2,3} | D. | {1,2,4} |
17.已知集合M={y|y=lgx,0<x<1},N={y|y=($\frac{1}{10}$)x,x>1},则M∩N=( )
| A. | {y|y<0} | B. | {y|y<$\frac{1}{10}$} | C. | {y|0<y<$\frac{1}{10}$} | D. | ∅ |
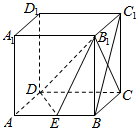 如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,
如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,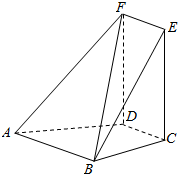 如图,在多面体EF-ABCD中,四边形ABCD,ABEF均为直角梯形,∠ABE=∠ABC=$\frac{π}{2}$,四边形DCEF为平行四边形,平面DCEF⊥平面ABCD.
如图,在多面体EF-ABCD中,四边形ABCD,ABEF均为直角梯形,∠ABE=∠ABC=$\frac{π}{2}$,四边形DCEF为平行四边形,平面DCEF⊥平面ABCD.