题目内容
10.已知不等式组$\left\{\begin{array}{l}{{x}^{2}-x-2>0}\\{2{x}^{2}+(5+2k)x+5k<0}\end{array}\right.$的整数解只有-2,则k的范围是( )| A. | -3≤k<2 | B. | -2≤k≤-1 | C. | -3<k<-1 | D. | -3≤k<0 |
分析 由x2-x-2>0,解得x>2或x<-1.由2x2+(5+2k)x+5k<0,化为(2x+5)(x+k)<0,对k分类讨论即可得出.
解答 解:由x2-x-2>0,解得x>2或x<-1.
由2x2+(5+2k)x+5k<0,
化为(2x+5)(x+k)<0,
当k>$\frac{5}{2}$时,不等式的解集为$-k<x<-\frac{5}{2}$,此时不等式组的解集为{x|$-k<x<-\frac{5}{2}$},其解集中不可能有-2,舍去.
当k=$\frac{5}{2}$时,不等式化为(2x+5)2<0,其解集为空集,因此不等式组的解集为空集,舍去.
当k<$\frac{5}{2}$时,不等式的解集为$-\frac{5}{2}<x<-k$,由于不等式组的解集中的整数解只有-2,∴-2<-k≤3,化为-3≤k<2,满足k<$\frac{5}{2}$,∴-3≤k<2.
综上可得:k的取值范围为:-3≤k<2.
故选:A.
点评 本题考查了一元二次不等式的解法、不等式组的解法、交集的运算性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
20.下列各组表示同-函数的是( )
| A. | y=x与y=$\sqrt{{x}^{2}}$ | B. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | ||
| C. | y=x+1与y=$\frac{{x}^{2}-1}{x-1}$ | D. | f(x)=x2-1与g(t)=t2-1 |
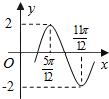 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).