题目内容

已知向量
a
，
b
，|
a
|=1，|
b
|=2，则|2
b
-
a
|的取值范围是
 
．
考点：向量的模
专题：平面向量及应用
分析：利用向量数量积运算性质、余弦函数的单调性即可得出．
解答： 解：设＜
a
，
b
＞=θ．
|2
b
-
a
|=
4
b
2+
a
2-4
a
•
b
=
4×22+1-4×2×1•cosθ
=
17-8cosθ

∵-1≤cosθ≤1，
∴9≤17-8cosθ≤25，
∴|2
b
-
a
|的取值范围是[3，5]．
故答案为：[3，5]．
点评：本题考查了向量数量积运算性质、余弦函数的单调性，属于基础题．
练习册系列答案
相关题目
过抛物线C：y2=2px（p＞0）上的点M分别向C的准线和x轴作垂线，两条垂线及C的准线和x轴围成边长为4的正方形，点M在第一象限．
（1）求抛物线C的方程及点M的坐标；
（2）过点M作倾斜角互补的两条直线分别与抛物线C交与A、B两点，且直线AB过点（0，-1），求△MAB的面积．
在△ABC中，AB=AC，延长AB到D，使BD=AB，AB的中点E，则
CD
CE
=
 
．
已知{an}是公比为2的等比数列，则
a1+a2+a3
a3+a4+a5
的值为
 
．
设A是△ABC中的最小角，且cosA=
a-1
2
，则实数a的取值范围是
 
．
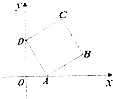如图，边长为1的正方形ABCD的顶点A，D分别在x轴，y轴正半轴上移动，则
OB
•
OC
≥1+
3
2
的概率为
 
．
函数f（x）=x2ex在区间（a，a+1）上存在极值点，则实数a的取值范围为
 
．
设D为不等式组
x≥0
x-y≤0
x+y-3≤0
所表示的平面区域，区域D上的点与点（1，0）之间的距离的最小值为
 
．
有以下叙述：
①半径为1的圆中，60°的圆心角所对的弧的长度为
π
3
；
②已知函数f（x）=
1+x2
1-x2
（x≠±1），则f（2）+f（3）+f（4）+f（
1
2
）+f（
1
3
）+f（
1
4
）=3；
③函数y=-tan（2x-
3π
4
）的单调递减区间是（
kπ
2
+
π
8
，
kπ
2
+
5π
8
），k∈Z；
④设集合A=[0，
1
2
），B=[
1
2
，1]，函数f（x）=
x+
1
2
(x∈A)
-2x+2(x∈B)
．若x0∈A，且f[f（x0）]∈A，则x0的取值范围是（
1
4
，
1
2
）．
其中所有正确叙述的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网