题目内容
12.已知sinθ+cosθ=2sinα,sinθcosθ=sin2β,求证:2cos2α=cos2β.分析 由同角三角函数关系式得到4cos2α-2=1-2sin2β,由此利用二倍角公式能证明2cos2α=cos2β.
解答 证明:∵sinθ+cosθ=2sinα,sinθcosθ=sin2β,
∴sin2θ+cos2θ+2sinθcosθ=1+2sin2β=4sin2α=4-4cos2α,
∴4cos2α-2=1-2sin2β,
∵2cos2α=2(2cos2α-1)=4cos2α-2,
cos2β=1-2sin2β,
∴2cos2α=cos2β.
点评 本题考查三角函数恒等式的证明,是中档题,解题时要认真审题,注意同角三角函数关系式和二倍角公式的合理运用.

练习册系列答案
相关题目
20.在矩形ABCD中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{BC}$|=2,则向量$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AC}$的长度等于( )
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 12 | D. | 6 |
4.等比数列{an}的前n项和为Sn,若公比q=4,S3=21,则( )
| A. | 4an=1-3Sn | B. | 4Sn=3an-1 | C. | 4Sn=3an+1 | D. | 4an=3Sn+1 |
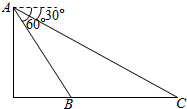 如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.
如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.