题目内容
设函数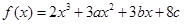 在
在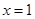 及
及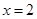 时取得极值.
时取得极值.
(1)求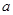 、b的值;
、b的值;
(2)若对于任意的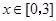 ,都有
,都有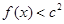 成立,求c的取值范围.
成立,求c的取值范围.
(1)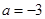 ,
,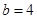 (2)
(2)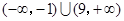
解析试题分析:解:(1)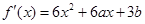 ,
,
因为函数 在
在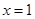 及
及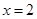 取得极值,则有
取得极值,则有 ,
,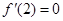 .
.
即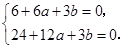
解得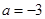 ,
,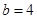 .
.
(2)由(1)可知,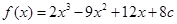 ,
,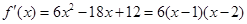 .
.
当 时,
时,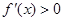 ;
;
当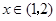 时,
时,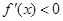 ;
;
当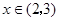 时,
时,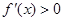 .
.
所以,当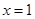 时,
时, 取得极大值
取得极大值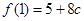 ,又
,又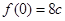 ,
, .
.
则当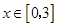 时,
时, 的最大值为
的最大值为 .
.
因为对于任意的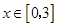 ,有
,有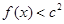 恒成立,
恒成立,
所以  ,
,
解得  或
或 ,
,
因此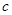 的取值范围为
的取值范围为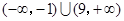 .
.
考点:导数的运用
点评:主要是根据导数的符号于函数单调性的关系来得到函数的极值和最值,得到求解,属于基础题。

练习册系列答案
相关题目
 ;
;
 在
在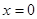 处取极值,求
处取极值,求 的值;
的值;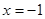 和
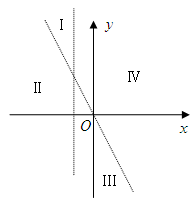
和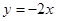 将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若
将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若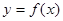 图象恰好位于其中一个区域,试判断其所在区域并求出相应的
图象恰好位于其中一个区域,试判断其所在区域并求出相应的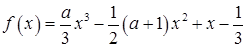 (
(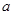
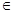 R).
R).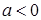 ,求函数
,求函数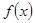 的极值;
的极值;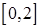 上有两个零点,若存在,求出
上有两个零点,若存在,求出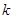 和
和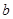 ,使得函数
,使得函数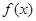 和
和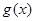 对其定义域上的任意实数
对其定义域上的任意实数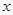 分别满足:
分别满足: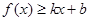 和
和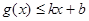 ,则称直线
,则称直线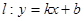 为
为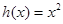 ,
,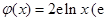 为自然对数的底数).
为自然对数的底数).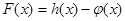 的极值;
的极值; 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由. .
. 时,求证:函数
时,求证:函数 在
在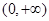 上单调递增;
上单调递增;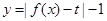 有三个零点,求
有三个零点,求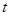 的值.
的值.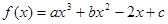 在
在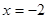 时有极大值6,在
时有极大值6,在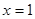 时有极小值
时有极小值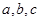 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.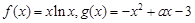 .
.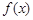 在
在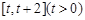 上的最小值;
上的最小值;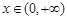 ,
,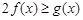 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.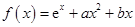 .
.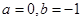 时,求
时,求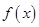 的单调区间;
的单调区间;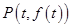
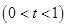 处的切线为
处的切线为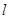 ,直线
,直线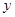 轴相交于点
轴相交于点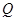 .若点
.若点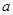 的取值范围.
的取值范围.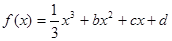 ,设曲线
,设曲线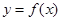 在与
在与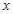 轴交点处的切线为
轴交点处的切线为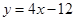 ,
,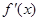 为
为 的导函数,满足
的导函数,满足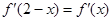 .
.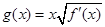 ,
,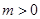 ,求函数
,求函数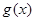 在
在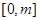 上的最大值;
上的最大值;