题目内容
已知函数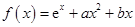 .
.
(Ⅰ)当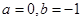 时,求
时,求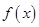 的单调区间;
的单调区间;
(Ⅱ)设函数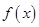 在点
在点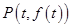
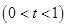 处的切线为
处的切线为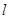 ,直线
,直线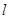 与
与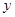 轴相交于点
轴相交于点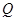 .若点
.若点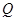 的纵坐标恒小于1,求实数
的纵坐标恒小于1,求实数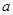 的取值范围.
的取值范围.
(Ⅰ)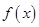 的单调递减区间为
的单调递减区间为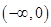 ,单调递增区间为
,单调递增区间为 (Ⅱ)
(Ⅱ)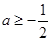
解析试题分析:(Ⅰ)当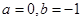 时,
时, ,
, , 1分
, 1分
所以,当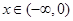 时,
时, ;当
;当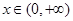 时,
时, ; 3分
; 3分
所以函数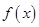 的单调递减区间为
的单调递减区间为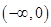 ,单调递增区间为
,单调递增区间为 . 4分
. 4分
(Ⅱ)因为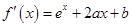 ,
,
所以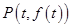 处切线的斜率
处切线的斜率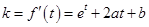 ,
,
所以切线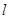 的方程为
的方程为 ,
,
令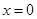 ,得
,得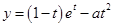
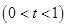 . 5分
. 5分
当 时,要使得点
时,要使得点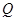 的纵坐标恒小于1,
的纵坐标恒小于1,
只需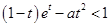 ,即
,即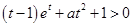
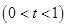 . 6分
. 6分
令 ,
,
则 , 7分
, 7分
因为 ,所以
,所以 ,
,
①若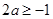 即
即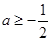 时,
时, ,
,
所以,当 时,
时, ,即
,即 在
在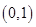 上单调递增,
上单调递增,
所以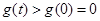 恒成立,所以
恒成立,所以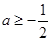 满足题意. 8分
满足题意. 8分
②若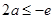 即
即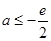 时,
时,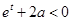 ,
,
所以,当 时,
时,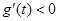 ,即
,即 在
在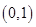 上单调递减,
上单调递减,
所以 ,所以
,所以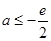 不满足题意. 9分
不满足题意. 9分
③若 即
即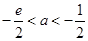 时,
时,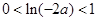 .
.
则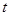 、
、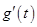 、
、 的关系如下表:
的关系如下表: 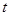


全真模拟试卷系列答案
阅读拓展与作文提优系列答案
单元提优测试卷系列答案
百渡期末综合测试系列答案
聊城中考系列答案
学业测评一卷通小学升学试题汇编系列答案
小学单元综合练习与检测系列答案
实验探究报告练习册系列答案
单元学习体验与评价系列答案
黄冈小状元小学升学考试冲刺复习卷系列答案
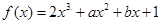 的导数为
的导数为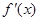 ,若函数
,若函数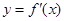 的图像关于直
的图像关于直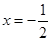 对称,且
对称,且 . (1)求实数
. (1)求实数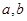 的值 ;(2)求函数
的值 ;(2)求函数 的极值.
的极值.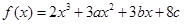 在
在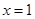 及
及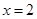 时取得极值.
时取得极值.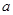 、b的值;
、b的值;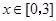 ,都有
,都有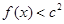 成立,求c的取值范围.
成立,求c的取值范围.
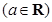 .
.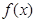 在定义域内的极值点的个数;
在定义域内的极值点的个数;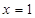 处取得极值,对
处取得极值,对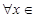
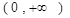 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 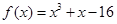 .
.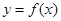 在点
在点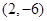 处的切线方程;
处的切线方程; 为曲线
为曲线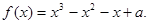
 的极值.
的极值.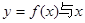 轴仅有一个交点.
轴仅有一个交点.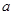 为实数,函数
为实数,函数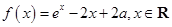 。
。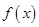 的单调区间与极值;
的单调区间与极值;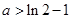 且
且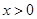 时,
时,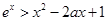 。
。 (2)
(2)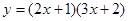
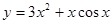 (4)
(4)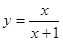
 .
.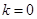 ,求
,求 的最小值;
的最小值;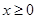 时
时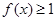 ,求实数
,求实数 的取值范围.
的取值范围.