题目内容
20．已知变量x，y满足$\left\{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}\right.$则目标函数z=$\frac{x+y+3}{x+2}$的最大值为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{5}{3}$ | C． | $\frac{5}{4}$ | D． | 1 |
分析 作出不等式组对应的平面区域，利用斜率的几何意义进行求解即可．
解答 
解：目标函数z=$\frac{x+y+3}{x+2}$=1+$\frac{y+1}{x+2}$，
作出不等式组对应的平面区域如图：
则$\frac{y+1}{x+2}$的几何意义是区域内的点到定点D（-2，-1）的斜率，
由图象知BD的斜率最大，则由$\left\{\begin{array}{l}{x-2y+4=0}\\{x+y-2=0}\end{array}\right.$得x=0，y=2，
即B（0，2），
此时BD的斜率kBD=$\frac{2+1}{0+2}$=$\frac{3}{2}$，
∴目标函数z=$\frac{x+y+3}{x+2}$的最大值为1+$\frac{3}{2}$=$\frac{5}{2}$，
故选：A．
点评 本题主要考查线性规划的基本应用，利用目标函数的几何意义结合直线的斜率公式是解决问题的关键，利用数形结合是解决问题的基本方法．
练习册系列答案
中考解读考点精练系列答案
相关题目
10．数列{an}满足a1=0，$\frac{1}{1-{a}_{n}}$-$\frac{1}{1-{a}_{n-1}}$=1（n≥2，n∈N*），则a2017=（ ）
| A． | $\frac{1}{2017}$ | B． | $\frac{1}{2016}$ | C． | $\frac{2016}{2017}$ | D． | $\frac{2015}{2016}$ |
11．已知i为虚数单位，若复数z满足（1-i）z=1+i，则|z|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
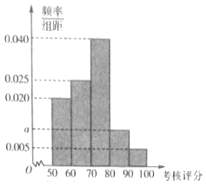2016年，某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》，为了解本省各家企业对环保的重视情况，从中抽取了40家企业进行考核评分，考核评分均在[50，100]内，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图（满分为100分）．