题目内容
11.在甲、乙等5位学生参加的一次社区专场演唱会中,每位学生的节目集中安排在一起演出,若采用抽签的方法随机确定各位学生的演出顺序(序号为1,2,3,4,5).(1)甲、乙两人的演出序号至少有一个为偶数的概率;
(2)甲、乙两人的演出序号不相邻的概率.
分析 (1)基本事件总数n=${A}_{5}^{5}$=120,甲、乙两人的演出序号至少有一个为偶数的对立事件为甲、乙两人的演出序号都是奇数,由此利用对立事件概率计算公式能求出甲、乙两人的演出序号至少有一个为偶数的概率.
(2)甲、乙两人的演出序号不相邻的对立事件是甲、乙两人的演出序号相邻,由此利用对立事件概率计算公式能求出甲、乙两人的演出序号不相邻的概率.
解答 解:(1)在甲、乙等5位学生参加的一次社区专场演唱会中,
每位学生的节目集中安排在一起演出,
采用抽签的方法随机确定各位学生的演出顺序(序号为1,2,3,4,5).
基本事件总数n=${A}_{5}^{5}$=120,
甲、乙两人的演出序号至少有一个为偶数的对立事件为甲、乙两人的演出序号都是奇数,
∴甲、乙两人的演出序号至少有一个为偶数的概率p1=1-$\frac{{A}_{3}^{2}{A}_{3}^{3}}{{A}_{5}^{5}}$=$\frac{7}{10}$.
(2)甲、乙两人的演出序号不相邻的对立事件是甲、乙两人的演出序号相邻,
∴甲、乙两人的演出序号不相邻的概率:
p2=1-$\frac{{A}_{4}^{4}{A}_{2}^{2}}{{A}_{5}^{5}}$=$\frac{3}{5}$.
点评 本题考查概率的求法,以及化简整理的运算能力,属于基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
19.要得到函数f(x)=sin2x的图象,只需将函数g(x)=cos2x的图象( )
| A. | 向左平移$\frac{π}{2}$个周期 | B. | 向右平移$\frac{π}{2}$个周期 | ||
| C. | 向左平移$\frac{π}{4}$个周期 | D. | 向右平移$\frac{π}{4}$个周期 |
20.已知变量x,y满足$\left\{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}\right.$则目标函数z=$\frac{x+y+3}{x+2}$的最大值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | 1 |
16.某地天气预报说:“明天本地降雨的概率为80%”,这是指( )
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
20.等比数列{an}中,a1>1,前n项和为Sn,若$\lim_{x→∞}{S_n}=\frac{1}{a_1}$,那么a1的取值范围是( )
| A. | (1,+∞) | B. | (1,2) | C. | $(1\;,\;\;\sqrt{3})$ | D. | $(1\;,\;\;\sqrt{2})$ |
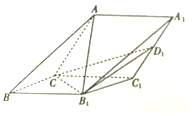 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.