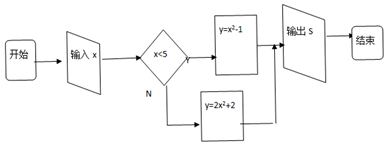
题目内容
12.在△ABC中,角A、B、C的对边分别为a,b,c,且2acosC-a=c-2ccosC,若c=3,则a+b的最大值为6.分析 2acosC-a=c-2ccosC,即2(a+c)cosC=a+c,可得cosC=$\frac{1}{2}$,C∈(0,π),解得C.再利用余弦定理与基本不等式的性质即可得出.
解答 解:∵2acosC-a=c-2ccosC,∴2(a+c)cosC=a+c,
∴cosC=$\frac{1}{2}$,C∈(0,π),
解得C=$\frac{π}{3}$.
由余弦定理可得:9=c2=a2+b2-2abcos$\frac{π}{3}$,
∴9=(a+b)2-3ab≥(a+b)2-3×$(\frac{a+b}{2})^{2}$,化为a+b≤6,当且仅当a=b=3时取等号.
∴a+b的最大值为6.
故答案为:6.
点评 本题考查了余弦定理、基本不等式的性质、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.函数y=f(x)图象上不同两点A(x1,y1),B(x2,y2)处的切线的斜率分别是kA,kB,规定φ(A,B)=$\frac{|{k}_{A}-{k}_{B}|}{|AB|}$叫做曲线在点A与点B之间的“弯曲度”.设曲线y=ex上不同的两点A(x1,y1),B(x2,y2),且x1-x2=1,若t•φ(A,B)<3恒成立,则实数t的取值范围是( )
| A. | (-∞,3] | B. | (-∞,2] | C. | (-∞,1] | D. | [1,3] |
20.已知变量x,y满足$\left\{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}\right.$则目标函数z=$\frac{x+y+3}{x+2}$的最大值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | 1 |
7.设命题p:函数f(x)=ln$\frac{{e}^{x}+1}{{e}^{-x}+1}$为奇函数;命题q:?x0∈(0,2),x${\;}_{0}^{2}$>2${\;}^{{x}_{0}}$,则下列命题为假命题的是( )
| A. | p∨q | B. | p∧(¬q) | C. | (¬p)∧q | D. | (¬p)∨(¬q) |
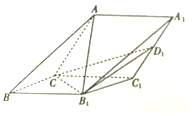 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.