Question

8．如图在△ABC中，AB=$\frac{{3\sqrt{6}}}{2}$，CD=5，∠ABC=45°，∠ACB=60°，则AD=7．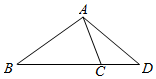

Answer 1

分析 过点A作AE⊥BC，垂足为E，分别求出AE=$\frac{3\sqrt{3}}{2}$，AC=3，再由余弦定理即可求出．

解答 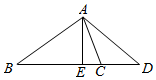解：过点A作AE⊥BC，垂足为E，
∵$AB=\frac{{3\sqrt{6}}}{2}，CD=5，∠ABC=45°，∠ACB=60°$，
在Rt△AEB中，AE=ABsinB=$\frac{3\sqrt{6}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{3}}{2}$，
在Rt△AEC中，AC=$\frac{AE}{sin∠ACB}$=$\frac{\frac{3\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}$=3，
由余弦定理可得，AD²=AC²+CD²-2AC•CDcos∠ACD=9+25-2×3×5×（-$\frac{1}{2}$）=49，
∴AD=7
故答案为：7．

点评 本题考查了解三角形和余弦定理，培养了学生的运算能力和分析解决问题的能力，属于基础题．