题目内容
3.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为$\sqrt{2}$,倾斜角为45°的直线l过点F.(1)求该椭圆的方程;
(2)若过点$M(1,\frac{1}{2})$的直线l与椭圆C相交于A,B两点,且M点恰为弦AB的中点,求直线l的方程.
分析 (1)求得抛物线的焦点,可得c=1,求出准线方程x=-1,可得与椭圆的一个交点,代入椭圆方程,解方程即可得到所求方程;
(2)设A(x1,y1),B(x2,y2),代入椭圆方程,运用点差法,结合中点坐标公式和直线的斜率公式,求得直线的斜率,再由点斜式方程即可得到所求方程.
解答 解:(1)抛物线y2=4x的焦点为F(1,0),准线方程为x=-1,
∴a2-b2=1 ①,
又椭圆截抛物线的准线x=-1所得弦长为$\sqrt{2}$,
∴得上交点为(-1,$\frac{\sqrt{2}}{2}$),∴$\frac{1}{{a}^{2}}$+$\frac{1}{2{b}^{2}}$=1②
由①代入②得2b4-b2-1=0,解得b2=1或b2=-$\frac{1}{2}$(舍去),
从而a2=b2+1=2,
∴该椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)点$M(1,\frac{1}{2})$,代入椭圆方程,可得$\frac{1}{2}$+$\frac{1}{4}$<1,即M在椭圆内,
直线AB与椭圆相交.
设A(x1,y1),B(x2,y2),代入椭圆方程可得,
x12+2y12=2,x22+2y22=2,
相减可得(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0,
由x1+x2=2,y1+y2=1,
可得直线AB的斜率为$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{2({y}_{1}+{y}_{2})}$=-1,
即有直线AB的方程为y-$\frac{1}{2}$=-(x-1),即为2x+2y-3=0.
点评 本题考查椭圆的方程的求法,注意运用抛物线的焦点和点满足椭圆方程,考查直线的方程的求法,注意运用点差法和中点坐标公式及直线的斜率公式,考查运算能力,属于中档题.

 同步奥数系列答案
同步奥数系列答案| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(Ⅱ)若用$\frac{y_i}{x_i}(i=1,2,3,4,5)$表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选3组,求这三组数据之和不超过20的概率.
(参考公式:$\widehat{y}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$)
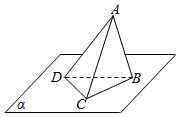 如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.
如右图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=2,AD=$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是$\sqrt{3}π$.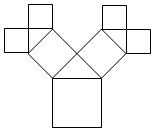 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$. 500辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过70km/h的汽车数量为50辆.
500辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过70km/h的汽车数量为50辆.