题目内容
18．椭圆$\frac{x^2}{36}+\frac{y^2}{20}=1$的两个焦点为F1、F2，弦AB经过F2，则△ABF1的周长为（ ）| A． | 22 | B． | 23 | C． | 24 | D． | 25 |
分析 利用椭圆定义求解．
解答 解：∵椭圆$\frac{x^2}{36}+\frac{y^2}{20}=1$的两个焦点为F1、F2，弦AB经过F2，
∴△ABF1的周长=4a=4×6=24．
故选：C．
点评 本题考查三角形周长的求法，是基础题，解题时要认真审题，注意椭圆性质的合理运用．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
9．设函数f（x）是定义在（-∞，0）上的可导函数，其导函数为f′（x），且有2f（x）+xf′（x）＜x，则不等式（x+1）2f（x+1）-4f（-2）＞0的解集为（ ）
| A． | （-∞，-2） | B． | （-2，-1） | C． | （-∞，-3） | D． | （-3，-1） |
在平面直角坐标系中，若点P（x，y）的坐标x，y均为整数，则称点P为格点，若一个多边形的顶点全是格点，则称该多边形为格点多边形．格点多边形的面积记为S，其内部的格点数记为N，边界上的格点数记为L．例如图中△ABC是格点三角形，对应的S=1，N=0，L=4．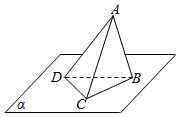
如右图，三棱锥A-BCD的顶点B、C、D在平面α内，CA=AB=BC=CD=DB=2，AD=$\sqrt{6}$，若将该三棱锥以BC为轴转动，到点A落到平面α内为止，则A、D两点所经过的路程之和是$\sqrt{3}π$．