题目内容
19.给出下列命题:①存在实数α,使$sinα•cosα=\frac{{\sqrt{3}}}{2}$
②函数$y=sin(\frac{3}{2}π-x)$是偶函数
③$x=\frac{π}{8}$是函数$y=cos(2x+\frac{3}{4}π)$的一条对称轴方程
④若α、β是第一象限的角,且α<β,则sinα<sinβ
其中正确命题的序号是②③.
分析 ①根据三角函数的有界性进行判断.
②根据三角函数的诱导公式进行化简即可.
③根据三角函数的对称性进行判断.
④根据三角函数值的大小关系进行比较即可.
解答 解:①∵sinαcosα=$\frac{1}{2}$sin2α∈[$-\frac{1}{2}$,$\frac{1}{2}$],∵$\frac{\sqrt{3}}{2}$>$\frac{1}{2}$,∴存在实数α,使$sinα•cosα=\frac{{\sqrt{3}}}{2}$错误,故①错误,
②函数$y=sin(\frac{3}{2}π-x)$=cosx是偶函数,故②正确,
③当$x=\frac{π}{8}$时,$y=cos(2x+\frac{3}{4}π)$=cos(2×$\frac{π}{8}$+$\frac{3π}{4}$)=cosπ=-1是函数的最小值,则$x=\frac{π}{8}$是函数$y=cos(2x+\frac{3}{4}π)$的一条对称轴方程,故③正确,
④当α=$\frac{π}{4}$,β=$\frac{9π}{4}$,满足α、β是第一象限的角,且α<β,但sinα=sinβ,即sinα<sinβ不成立,故④错误,
故答案为:②③.
点评 本题主要考查命题的真假判断,涉及三角函数的图象和性质,考查学生的运算和推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)<x,则不等式(x+1)2f(x+1)-4f(-2)>0的解集为( )
| A. | (-∞,-2) | B. | (-2,-1) | C. | (-∞,-3) | D. | (-3,-1) |
4.班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出计算式即可,不必计算出结果)
(Ⅱ)随机抽取8位,他们的数学分数从小到大排序是:60,65,70,75,80,85,90,95,物理分数从小到大排序是:72,77,80,84,88,90,93,95.
(i)若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(ii)若这8位同学的数学、物理分数事实上对应如下表:
根据上表数据,用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱.如果具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关性,请说明理由.
参考公式:相关系数r=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}\sum_{i=1}^n{{{({y_i}-\overline y)}^2}}}}}}$;回归直线的方程是:$\widehaty=bx+a$,其中对应的回归估计值b=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,a=$\overline y-b\overline x$,$\widehat{y_i}$是与xi对应的回归估计值.
参考数据:$\overline x=77.5,\overline y=84.875,{\sum_{i=1}^8{({x_i}-\overline x)}^2}≈1050,{\sum_{i=1}^8{({y_i}-\overline y)}^2}$≈457,$\sum_{i=1}^8{({x_i}-\overline x)}({y_i}-\overline y)≈688,\sqrt{1050}≈32.4,\sqrt{457}≈21.4,\sqrt{550}$≈23.5.
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出计算式即可,不必计算出结果)
(Ⅱ)随机抽取8位,他们的数学分数从小到大排序是:60,65,70,75,80,85,90,95,物理分数从小到大排序是:72,77,80,84,88,90,93,95.
(i)若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(ii)若这8位同学的数学、物理分数事实上对应如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
参考公式:相关系数r=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}\sum_{i=1}^n{{{({y_i}-\overline y)}^2}}}}}}$;回归直线的方程是:$\widehaty=bx+a$,其中对应的回归估计值b=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,a=$\overline y-b\overline x$,$\widehat{y_i}$是与xi对应的回归估计值.
参考数据:$\overline x=77.5,\overline y=84.875,{\sum_{i=1}^8{({x_i}-\overline x)}^2}≈1050,{\sum_{i=1}^8{({y_i}-\overline y)}^2}$≈457,$\sum_{i=1}^8{({x_i}-\overline x)}({y_i}-\overline y)≈688,\sqrt{1050}≈32.4,\sqrt{457}≈21.4,\sqrt{550}$≈23.5.
9.Sn是等差数列{an}的前n项和,如果S10=120,那么a3+a8的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
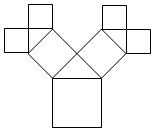 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到4095个正方形,设初始正方形的边长为$\frac{\sqrt{2}}{2}$,则最小正方形的边长为$\frac{1}{64}$.