题目内容
如图,设P是圆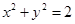 上的动点,点
上的动点,点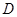 是
是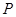 在
在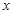 轴上的投影,
轴上的投影,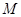 为线段PD上
为线段PD上 一点,且
一点,且 .点
.点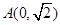 、
、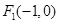 .
.
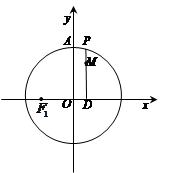
(1)设在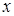 轴上存在定点
轴上存在定点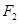 ,使
,使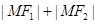 为定值,试求
为定值,试求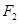 的坐标,并指出定值是多少?
的坐标,并指出定值是多少?
(2)求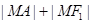 的最大值,并求此时点
的最大值,并求此时点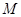 的坐标.
的坐标.
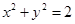 上的动点,点
上的动点,点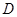 是
是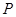 在
在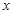 轴上的投影,
轴上的投影,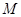 为线段PD上
为线段PD上 一点,且
一点,且 .点
.点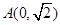 、
、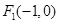 .
.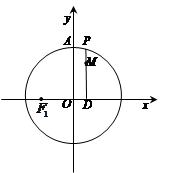
(1)设在
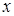 轴上存在定点
轴上存在定点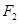 ,使
,使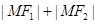 为定值,试求
为定值,试求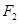 的坐标,并指出定值是多少?
的坐标,并指出定值是多少?(2)求
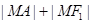 的最大值,并求此时点
的最大值,并求此时点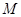 的坐标.
的坐标.(1)设点M的坐标是 ,P的坐标是
,P的坐标是

因为点D是P在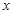 轴上投影,
轴上投影,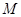 为PD上一点,由条件得:
为PD上一点,由条件得: ,且
,且 ---2f
---2f
∵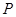 在圆
在圆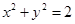 上,∴
上,∴ ,整理得
,整理得 ,
,
即M轨迹是以 为焦点的椭圆
为焦点的椭圆
由椭圆的定义可知,
(2)由(1)知,
当 三点共线,且
三点共线,且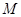 在
在 延长线上时,取等号.
延长线上时,取等号.
直线 ,联立
,联立 ,
,
其中 ,解得
,解得
即所求的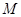 的坐标是
的坐标是 .
.
 ,P的坐标是
,P的坐标是

因为点D是P在
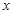 轴上投影,
轴上投影,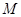 为PD上一点,由条件得:
为PD上一点,由条件得: ,且
,且 ---2f
---2f∵
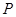 在圆
在圆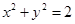 上,∴
上,∴ ,整理得
,整理得 ,
,
即M轨迹是以
 为焦点的椭圆
为焦点的椭圆由椭圆的定义可知,

(2)由(1)知,

当
 三点共线,且
三点共线,且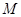 在
在 延长线上时,取等号.
延长线上时,取等号.直线
 ,联立
,联立 ,
,其中
 ,解得
,解得
即所求的
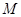 的坐标是
的坐标是 .
.略

练习册系列答案
相关题目
 与圆
与圆 相交于M,N两点,若
相交于M,N两点,若 ,则k的取值范围是_______________
,则k的取值范围是_______________ 在点
在点 处的切线方程为
处的切线方程为



 的点共有( )
的点共有( )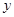 轴相切,圆心在直线
轴相切,圆心在直线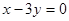 上,在
上,在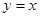 上截得的弦长为
上截得的弦长为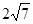 ,
,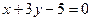 相切于点
相切于点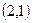 .
. 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  的圆
的圆 的切线方程是_____________。
的切线方程是_____________。 与圆
与圆 相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为_________________
相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为_________________