题目内容
16.已知奇函数$f(x)=a-\frac{1}{{{2^x}+1}}\;,\;\;x∈({-1\;,\;\;1})$.(Ⅰ)求a的值;
(Ⅱ)若函数f(x)满足f(x-1)+f(x)<0,求x的取值范围.
分析 (Ⅰ)根据f(x)是定义在(-1,1)上的奇函数,得出f(0)=0,求出a值;
(Ⅱ)写出f(x)的解析式,根据f(x)的定义与解析式,把不等式f(x-1)+f(x)<0化为关于x的不等式组,求出解集即可.
解答 解:(Ⅰ)由f(x)=a-$\frac{1}{{2}^{x}+1}$是(-1,1)上的奇函数,
∴f(0)=a-$\frac{1}{{2}^{0}+1}$=0,
解得a=$\frac{1}{2}$;
(Ⅱ)由(Ⅰ)知,
f(x)=$\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$,且x∈(-1,1),
又f(x)满足f(x-1)+f(x)<0,
即$\left\{\begin{array}{l}{-1<x<1}\\{-1<x-1<1}\\{\frac{1}{2}-\frac{1}{{2}^{x-1}+1}+\frac{1}{2}-\frac{1}{{2}^{x}+1}<0}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{0<x<1}\\{{2}^{2x}<2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{0<x<1}\\{x<\frac{1}{2}}\end{array}\right.$,
即0<x<$\frac{1}{2}$,
∴x的取值范围是(0,$\frac{1}{2}$).
点评 本题考查了奇函数的定义与指数函数的运算问题,也考查了不等式的解法与应用问题,是综合性题目.

练习册系列答案
相关题目
6.函数f(x)=$\frac{{e}^{2x}}{x}$的导函数为( )
| A. | f′(x)=2e2x | B. | f′(x)=$\frac{(2x-1){e}^{2x}}{{x}^{2}}$ | C. | f′(x)=$\frac{2{e}^{2x}}{x}$ | D. | f′(x)=$\frac{(x-1){e}^{2x}}{{x}^{2}}$ |
6.执行如图所示的程序框图,则输出的结果为( )
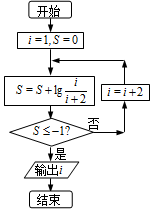

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
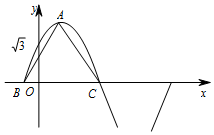 已知函数$f(x)=Asin({ωx+φ})({A>0\;,\;\;ω>0\;,\;\;|φ|<\frac{π}{2}})$在一个周期内的图象如图所示,图象过点$({0\;,\;\;\sqrt{3}})$,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为高为$2\sqrt{3}$的正三角形.
已知函数$f(x)=Asin({ωx+φ})({A>0\;,\;\;ω>0\;,\;\;|φ|<\frac{π}{2}})$在一个周期内的图象如图所示,图象过点$({0\;,\;\;\sqrt{3}})$,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为高为$2\sqrt{3}$的正三角形.