题目内容
|x-a|+
≥
对一切x>0恒成立,则a的范围( )
| 1 |
| x |
| 1 |
| 2 |
| A、a≤2 | ||
B、a≤
| ||
| C、a≤1 | ||
D、a≤
|
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:把|x-a|+
≥
对一切x>0恒成立,转化为两个函数y=|x-a|与y=
-
的图象问题,数形结合即可求出a的取值范围.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
解答:
解:由|x-a|+
≥
,得|x-a|≥
-
,
|x-a|+
≥
对一切x>0恒成立,转化为当x>0时,函数y=|x-a|的函数值恒大于等于y=
-
的函数值,
对应的图象如图,
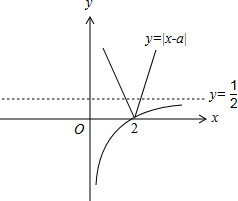
由图可知a的取值范围是(-∞,2].
故选:A.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
|x-a|+
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
对应的图象如图,

由图可知a的取值范围是(-∞,2].
故选:A.
点评:本题主要考查不等式恒成立问题,这类题目往往转化为最值问题解决,还考查了基本不等式及转化思想,分类讨论等思想方法,数形结合的方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a,b是夹角为30°的异面直线,则满足条件“a⊆α,b⊆β,且α⊥β”的平面α,β( )
| A、不存在 | B、有且只有一对 |
| C、有且只有两对 | D、有无数对 |
对?x,y∈R,函数f(x)满足f(x+y)=f(x)+f(y)+1,f(1)=a(a为大于0的常数),已知an=f(n)(n∈N*),则下列结论一定正确的是( )
| A、数列{lgan}为等差数列 |
| B、数列{lgan}为等比数列 |
| C、数列{e an}为等差数列 |
| D、数列{e an}为等比数列 |
