题目内容
2010年上海世博会是世博会历史上首次在发展中国家举办的综合性世博会,上海世博会的主题是:城市,让生活更美好,大会期间,某超市的世博会吉祥物海宝在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t(件),价格近似满足f(t)=20-
|t-10|(元).
(1)试写出“海宝”的日销售额y与时间t(0<t≤20)的函数表达式;
(2)求“海宝”的日销售额y的最大值与最小值.
| 1 |
| 2 |
(1)试写出“海宝”的日销售额y与时间t(0<t≤20)的函数表达式;
(2)求“海宝”的日销售额y的最大值与最小值.
考点:函数模型的选择与应用,函数的最值及其几何意义
专题:计算题,应用题,函数的性质及应用
分析:(1)由题意,y=g(t)•f(t)=(80-2t)(20-
|t-10|)=
;
(2)分别求当0<t≤10时,当10<t≤20时的最值,从而求最值.
| 1 |
| 2 |
|
(2)分别求当0<t≤10时,当10<t≤20时的最值,从而求最值.
解答:
解:(1)由题意,
y=g(t)•f(t)
=(80-2t)(20-
|t-10|)
=
;
(2)当0<t≤10时,
y=-t2+10t+1200在t=5时有最大值y=1225,
当t=10时有最小值1200;
当10<t≤20时,
y=t2-90t+2000在(10,20]上是减函数,
当t=20时有最小值600;
y<100-900+2000=1200;
故“海宝”的日销售额y的最大值为1225元,
最小值为600元.
y=g(t)•f(t)
=(80-2t)(20-
| 1 |
| 2 |
=
|
(2)当0<t≤10时,
y=-t2+10t+1200在t=5时有最大值y=1225,
当t=10时有最小值1200;
当10<t≤20时,
y=t2-90t+2000在(10,20]上是减函数,
当t=20时有最小值600;
y<100-900+2000=1200;
故“海宝”的日销售额y的最大值为1225元,
最小值为600元.
点评:本题考查了分段函数在实际问题中的应用,属于中档题.

练习册系列答案
相关题目
已知a>0,b>0,且4a-b≥0,若函数f(x)=
ax3+x2+bx无极值,则
的取值范围为( )
| 1 |
| 3 |
| b-2 |
| a+1 |
A、[2
| ||
B、[2
| ||
C、[-2
| ||
D、[-2
|
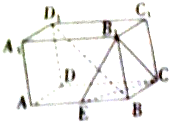 如图所示,长方体ABCD-A1B1C1D1的侧面BCC1B1是正方形,E是AB的中点,AB=
如图所示,长方体ABCD-A1B1C1D1的侧面BCC1B1是正方形,E是AB的中点,AB=