题目内容
6.已知数列{an}中,an>0,a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,a100=a96,则a2016+a3=( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{1+\sqrt{5}}}{2}$ | C. | $\frac{{-1+\sqrt{5}}}{2}$ | D. | $\frac{5}{2}$ |
分析 a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,可得a3=$\frac{1}{{a}_{1}+1}$.由于a100=a96,${a}_{100}=\frac{1}{{a}_{98}+1}$,a98=$\frac{1}{{a}_{96}+1}$,化为${a}_{100}=\frac{{a}_{100}+1}{{a}_{100}+2}$,an>0,解得${a}_{100}=\frac{\sqrt{5}-1}{2}$,可得a100=a1004=…=a100+4×479=a2016,即可得出.
解答 解:∵a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,∴a3=$\frac{1}{{a}_{1}+1}$=$\frac{1}{2}$.
∵a100=a96,${a}_{100}=\frac{1}{{a}_{98}+1}$,a98=$\frac{1}{{a}_{96}+1}$,化为${a}_{100}=\frac{{a}_{96}+1}{{a}_{96}+2}$,即${a}_{100}=\frac{{a}_{100}+1}{{a}_{100}+2}$,an>0,解得${a}_{100}=\frac{\sqrt{5}-1}{2}$,
∴a100=a1004=…=a100+4×479=a2016=$\frac{\sqrt{5}-1}{2}$.
∴a2016+a3=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查了递推关系的应用、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.将二次函数y=x2的图象向左平移2个单位,再向下平移3个单位,得到的函数的解析式为( )
| A. | y=x2+4x+7 | B. | y=x2+4x+1 | C. | y=x2-4x+7 | D. | y=x2-4x-7 |
17.正定中学教学处采用系统抽样方法,从学校高三年级全体800名学生中抽50名学生做学习状况问卷调查.现将800名学生从1到800进行编号,在1~16中随机抽取一个数,如果抽到的是7,则从41~56中应取的数是( )
| A. | 47 | B. | 48 | C. | 54 | D. | 55 |
1.已知实数x,y满足$\left\{\begin{array}{l}{x-y+3≥0}\\{x+y-1≥0}\\{x≤1}\end{array}\right.$,若直线x+ky-1=0将可行域分成面积相等的两部分,则实数k的值为( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
11.已知等差数列{an}满足a1+a2+a3+…+a101=0,则有( )
| A. | a1+a101>0 | B. | a2+a100<0 | C. | a3+a99=0 | D. | a51=51 |
15.若正数a,b满足a+b=2,则$\frac{1}{a+1}$+$\frac{4}{b+1}$的最小值是( )
| A. | 1 | B. | $\frac{9}{4}$ | C. | 9 | D. | 16 |
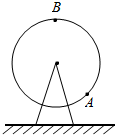 乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.
乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.