题目内容
2.曲线y=($\frac{1}{2}$)x在x=0点处的切线方程是( )| A. | x+yln 2-ln 2=0 | B. | x-y+1=0 | C. | xln 2+y-1=0 | D. | x+y-1=0 |
分析 求出函数的导数,计算x=0时,y以及y′的值,代入切线方程即可.
解答 解:y=($\frac{1}{2}$)x,y′=${(\frac{1}{2})}^{x}$ln$\frac{1}{2}$,
故x=0时,y=1,y′=-ln2,
故切线方程是:y-1=-ln2(x-0),
即xln2+y-1=0,
故选:C.
点评 本题考查了求曲线的切线方程问题,求出直线的斜率以及切点是解题的关键,本题是一道基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
10.p:log2a>0是q:$\frac{1}{a}$<1 的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.不等式kx2-kx+1>0对一切实数x均成立,则k的取值范围是( )
| A. | 0<k<4 | B. | 0≤k<4 | C. | 0<k≤4 | D. | 0≤k≤4 |
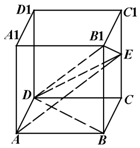 在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.