题目内容
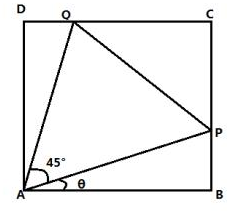 如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.
如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.(1)试用t表示线段PQ;
(2)探究△QAP的周长是否为定值;
(3)试求四边形APCQ面积的最大值.
考点:函数解析式的求解及常用方法,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)利用已知条件,结合直角三角形,直接用t表示出PQ的长度,
(2)设△QAP的周长为l,l=CP+CQ+PQ,然后推出△CPQ的周长l为定值,
(3)设四边形APCQ面积为S,S=S正方形ABCD-S△ABP-S△ADQ,利用基本不等式求出最值.
(2)设△QAP的周长为l,l=CP+CQ+PQ,然后推出△CPQ的周长l为定值,
(3)设四边形APCQ面积为S,S=S正方形ABCD-S△ABP-S△ADQ,利用基本不等式求出最值.
解答:
解:(1)∵∠PAB=θ,且tanθ=t,∠PAQ=45°,正方形ABCD边长为1
∴BP=t,0≤t≤1,∠DAQ=45°-θ,DQ=tan(45°-θ)=
,
∴CQ=1-
=
,
∴PQ=
=
=
.
(2)设△QAP的周长为l,
l=CP+CQ+PQ
=1-t+
+
=1-t+1+t=2.
∴△QAP的周长为定值.
(3)设四边形APCQ面积为S,
∴S=S正方形ABCD-S△ABP-S△ADQ
=1-
-
•
=2-
(t+1+
)
≤2-
.
当t=
-1时取等号,
故四边形APCQ面积的最大值为2-
.
∴BP=t,0≤t≤1,∠DAQ=45°-θ,DQ=tan(45°-θ)=
| 1-t |
| 1+t |
∴CQ=1-
| 1-t |
| 1+t |
| 2t |
| 1+t |
∴PQ=
| CP2+CQ2 |
(1-t)2+(
|
| 1+t2 |
| 1+t |
(2)设△QAP的周长为l,
l=CP+CQ+PQ
=1-t+
| 2t |
| 1+t |
| 1+t2 |
| 1+t |
=1-t+1+t=2.
∴△QAP的周长为定值.
(3)设四边形APCQ面积为S,
∴S=S正方形ABCD-S△ABP-S△ADQ
=1-
| t |
| 2 |
| 1 |
| 2 |
| 1-t |
| 1+t |
| 1 |
| 2 |
| 2 |
| t+1 |
≤2-
| 2 |
当t=
| 2 |
故四边形APCQ面积的最大值为2-
| 2 |
点评:本题考查三角形的实际应用,函数值的求法,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
(x2+
-2)4的展开式中常数项是( )
| 1 |
| x2 |
| A、30 | B、40 | C、70 | D、120 |