题目内容
已知圆M：x2+（y-2）2=1，直线l：y=-1，动圆P与圆M相外切，且与直线l切，设动圆圆心P的轨迹为E．
（Ⅰ）求E的方程；
（Ⅱ）若点A，B是E上的两个动点，O为坐标原点，且
•
=-16，求证：直线AB恒过定点．
（Ⅰ）求E的方程；
（Ⅱ）若点A，B是E上的两个动点，O为坐标原点，且
| OA |
| OB |
考点：直线和圆的方程的应用,轨迹方程
专题：综合题,直线与圆
分析：（Ⅰ）根据动圆P与直线y=-1相切，且与定圆M：x2+（y-2）2=1外切，可得动动点P到M（0，2）的距离与到直线y=-2的距离相等，由抛物线的定义知，点P的轨迹是抛物线，由此易得轨迹方程；
（Ⅱ）设直线AB：y=kx+b，将直线AB代入到x2=8y中得x2-8kx-8b=0，利用韦达定理，结合
•
=-16，求出b，即可证明直线AB恒过定点．
（Ⅱ）设直线AB：y=kx+b，将直线AB代入到x2=8y中得x2-8kx-8b=0，利用韦达定理，结合
| OA |
| OB |
解答：
（Ⅰ）解：由题意动圆P与直线y=-1相切，且与定圆M：x2+（y-2）2=1外切
所以动点P到M（0，2）的距离与到直线y=-2的距离相等
由抛物线的定义知，点P的轨迹是以C（0，2）为焦点，直线y=-2为准线的抛物线
故所求P的轨迹方程为：x2=8y． …（4分）
（Ⅱ）证明：设直线AB：y=kx+b，A（x1，y1），B（x2，y2），
将直线AB代入到x2=8y中得x2-8kx-8b=0，
所以x1+x2=8k，x1x2=-8b…（6分）
又因为
•
=x1x2+y1y2=x1x2+
=-8b+b2=-16，
∴b=4，…（10分）
∴恒过定点（0，4）． …（12分）
所以动点P到M（0，2）的距离与到直线y=-2的距离相等
由抛物线的定义知，点P的轨迹是以C（0，2）为焦点，直线y=-2为准线的抛物线
故所求P的轨迹方程为：x2=8y． …（4分）
（Ⅱ）证明：设直线AB：y=kx+b，A（x1，y1），B（x2，y2），
将直线AB代入到x2=8y中得x2-8kx-8b=0，
所以x1+x2=8k，x1x2=-8b…（6分）
又因为
| OA |
| OB |
| x12x22 |
| 64 |
∴b=4，…（10分）
∴恒过定点（0，4）． …（12分）
点评：本题考查轨迹方程，考查直线与抛物线的位置关系，考查转化思想与计算能力，熟记抛物线的定义是求解本题的关键．
练习册系列答案
相关题目
如图，已知圆E：（x+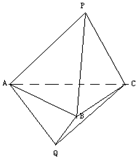
如图，在六面体PABCQ中，QA=QB=QC=AB=CB=CA=