题目内容
在△ABC中,a,b,c为角A,B,C所对的边,且(b-2c)cosA=a-2acos2
.
(1)求角A的值;
(2)若BC边上的中线长为
,求b+c的最大值.
| B |
| 2 |
(1)求角A的值;
(2)若BC边上的中线长为
| 3 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)已知等式右边变形后,利用二倍角的余弦函数公式化简,再利用正弦定理化简两边,整理求出cosA的值,即可确定出A的度数;
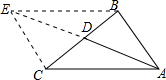
(2)延长AD到E,使ED=AD=
,连接EB,EC,可得出△CDE≌△BDA,在三角形ACE中,利用余弦定理列出关系式,并利用基本不等式变形求出bc的最大值,利用完全平方公式化简(b+c)2=b2+c2+2bc,确定出b+c的范围,即可求出最大值.
(2)延长AD到E,使ED=AD=
| 3 |
解答:
 解:(1)已知等式变形得:(b-2c)cosA=a-2acos2
解:(1)已知等式变形得:(b-2c)cosA=a-2acos2
=-a(2cos2
-1)=-acosB,
利用正弦定理化简得:(sinB-2sinC)cosA=-sinAcosB,
去括号整理得:sinAcosB+cosAsinB=2sinCcosA,即sin(A+B)=sinC=2sinCcosA,
∵sinC≠0,∴cosA=
,
则A=
;
(2)延长AD到E,使ED=AD=
,连接EB,EC,可得出△CDE≌△BDA,
在三角形ACE中,∠ACE=
,AE=2AD=2
,EC=AB=c,CA=b,
由余弦定理得:AE2=AC2+AB2-2AC•ABcosA=AC2+AB2-AC•AB=b2+c2-bc=2bc-bc≥bc,即bc≤AE2=12,
∴(b+c)2=b2+c2+2bc=AE2+3bc≤12+36=48,
∴2
<b+c≤4
,
则b+c的最大值为4
.
 解:(1)已知等式变形得:(b-2c)cosA=a-2acos2
解:(1)已知等式变形得:(b-2c)cosA=a-2acos2| B |
| 2 |
| B |
| 2 |
利用正弦定理化简得:(sinB-2sinC)cosA=-sinAcosB,
去括号整理得:sinAcosB+cosAsinB=2sinCcosA,即sin(A+B)=sinC=2sinCcosA,
∵sinC≠0,∴cosA=
| 1 |
| 2 |
则A=
| π |
| 3 |
(2)延长AD到E,使ED=AD=
| 3 |
在三角形ACE中,∠ACE=
| 2π |
| 3 |
| 3 |
由余弦定理得:AE2=AC2+AB2-2AC•ABcosA=AC2+AB2-AC•AB=b2+c2-bc=2bc-bc≥bc,即bc≤AE2=12,
∴(b+c)2=b2+c2+2bc=AE2+3bc≤12+36=48,
∴2
| 3 |
| 3 |
则b+c的最大值为4
| 3 |
点评:此题考查了正弦、余弦定理,以及基本不等式的运用,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
⊙O1:x2+y2=1与⊙O2:(x-3)2+(y+4)2=9,则⊙O1与⊙O2的位置关系为( )
| A、相交 | B、外切 | C、内切 | D、外离 |
 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥面ABCD,E为PD之中点,PA=2AB=2
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥面ABCD,E为PD之中点,PA=2AB=2