题目内容
已知下列不等式①x2-4x+3＜0；②x2-6x+8＜0；③x2-9x+a＜0，要使①②同时成立的x也满足③，求a的范围．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：联立①②得
，解得2＜x＜3．由于2＜x＜3也满足③x2-9x+a＜0，可得③的解集非空且（2，3）是③解集的子集．
|
解答：
解：联立①②得
，解得2＜x＜3．
∵2＜x＜3也满足③x2-9x+a＜0，
∴③的解集非空且（2，3）是③解集的子集．
由f（x）=x2-9x+a＜0，
∴f（2）=-14+a≤0，且f（3）=-18+a≤0，解得a≤14．
∴a的范围是（-∞，14]．
|
∵2＜x＜3也满足③x2-9x+a＜0，
∴③的解集非空且（2，3）是③解集的子集．
由f（x）=x2-9x+a＜0，
∴f（2）=-14+a≤0，且f（3）=-18+a≤0，解得a≤14．
∴a的范围是（-∞，14]．
点评：本题考查了不等式组的解法、集合之间的关系，考查了推理能力和计算能力，属于中档题．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
若AD为△ABC的中线，现有质地均匀的粒子散落在△ABC内，则粒子在△ABD内的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
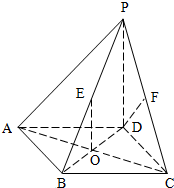已知在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧棱PD⊥平面ABCD，且PD=2，O为底面对角线的交点，E、F分别为棱PB，PC的中点