题目内容
7.已知在直角梯形ABCD中,AB⊥AD,CD⊥AD,AB=2AD=2CD=2,将直角梯形ABCD沿AC折叠成三棱锥D-ABC,当三棱锥D-ABC的体积取最大值时,其外接球的体积为$\frac{4π}{3}$.分析 画出图形,确定三棱锥外接球的半径,然后求解外接球的体积即可.
解答 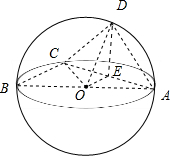 解:已知直角梯形ABCD,AB⊥AD,CD⊥AD,AB=2AD=2CD=2,沿AC折叠成三棱锥,如图:AB=2,AD=1,CD=1,
解:已知直角梯形ABCD,AB⊥AD,CD⊥AD,AB=2AD=2CD=2,沿AC折叠成三棱锥,如图:AB=2,AD=1,CD=1,
∴AC=$\sqrt{2}$,BC=$\sqrt{2}$,
∴BC⊥AC,
取AC的中点E,AB的中点O,连结DE,OE,∵当三棱锥体积最大时,
∴平面DCA⊥平面ACB,
∴OB=OA=OC=OD,
∴OB=1,就是外接球的半径为1,
此时三棱锥外接球的体积:$\frac{4π}{3}×{1}^{3}$=$\frac{4π}{3}$.
故答案为:$\frac{4π}{3}$.
点评 本题考查折叠问题,三棱锥的外接球的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
18.已知集合M={x|x2-2x-3<0},N={x|x>a}若M⊆N,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,-1) | C. | [3,+∞) | D. | (3,+∞) |
19.“?x∈R,x2+ax+1≥0成立”是“|a|≤2”的( )
| A. | 充分必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分而不必要条件 | D. | 既不充分也不必要条件 |
 已知抛物线y2=2px(p>0),四边形ABCD内接于抛物线,如图所示.
已知抛物线y2=2px(p>0),四边形ABCD内接于抛物线,如图所示.