题目内容
20.画出下列函数在长度为一个周期的闭区间上的简图(有条件的可用计算器或计算机作图检验):(1)y=4sin$\frac{1}{2}$x,x∈R;
(2)y=$\frac{1}{2}$cos3x,x∈R;
(3)y=3sin(2x+$\frac{π}{6}$),x∈R);
(4)y=2cos($\frac{1}{2}$x-$\frac{1}{4}$π),x∈R.
分析 用五点法作出各个函数在一个周期上的简图.
解答 解:(1)对于函数y=4sin$\frac{1}{2}$x,x∈R,列表:
| $\frac{1}{2}$x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 0 | π | 2π | 3π | 4π |
| y | 0 | 4 | 0 | -4 | 0 |

(2)对于函数y=$\frac{1}{2}$cos3x,x∈R,列表:
| 3x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 0 | $\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| y | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ |

(3)对于函数y=3sin(2x+$\frac{π}{6}$),x∈R),列表:
| 2x+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| y | 0 | 3 | 0 | -3 | 0 |

(4)对于函数y=2cos($\frac{1}{2}$x-$\frac{1}{4}$π),x∈R,列表:
| $\frac{1}{2}$x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| y | 2 | 0 | -2 | 0 | 2 |

点评 本题主要考查用五点法作出正弦函数、余弦函数在一个周期上的简图,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
9.如果X~B(15,$\frac{1}{4}$),则使P(X=k)取最大值的k的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 3或4 |
 如图,A,B,C,D四点共圆,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A,B,C,D四点共圆,BC与AD的延长线交于点E,点F在BA的延长线上.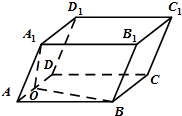 在平行六面体ABCD-A1B1C1D1中,AA1=AD=AB=2,∠A1AD=∠DAB=60°,O是AD的中点.
在平行六面体ABCD-A1B1C1D1中,AA1=AD=AB=2,∠A1AD=∠DAB=60°,O是AD的中点.