Question

10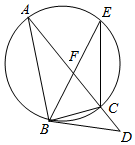．如图，△ABC为圆的内接三角形，∠ABC的平分线BF交圆于点E，过点B作圆的切线交AC的延长线于点D
（Ⅰ）证明：BD=DF；
（Ⅱ）若∠D=∠EBC，求证：$\frac{A{B}^{2}}{B{D}^{2}}$=$\frac{AF}{CD}$．

Answer 1

分析 （Ⅰ）证明∠CFB=∠DBF，即可证明BD=DF；
（Ⅱ）证明BD²=AD×DC，AB²=AD×AF，即可证明$\frac{A{B}^{2}}{B{D}^{2}}$=$\frac{AF}{CD}$．

解答 证明：（Ⅰ）∵过点B作圆的切线交AC的延长线于点D，
∴∠CBD=∠A，
∵∠ABC的平分线BF交圆于点E，
∴∠ABF=∠CBF，
∵∠CFB=∠A+∠ABF，
∴∠CFB=∠DBF，
∴BD=DF；
（Ⅱ）∵BD是切线，
∴∠DBC=∠A，
又∵∠BDC=∠ADB，
∴△BDC∽△ADB，
∴$\frac{BD}{AD}=\frac{DC}{DB}=\frac{BC}{AB}$，
∴BD²=AD×DC，$\frac{BD}{BC}=\frac{AD}{AB}$
∵∠D=∠EBC，∠CFB=∠DBF，∠ACB=∠CBD+∠D
∴△DBF∽△BCF，
∴$\frac{DB}{BC}=\frac{BF}{CF}$，
∵$\frac{BD}{BC}=\frac{AD}{AB}$，
∴$\frac{BF}{CF}$=$\frac{AD}{AB}$，
∵BF=BC，
∴$\frac{BC}{CF}$=$\frac{AD}{AB}$，
∵∠ABC的平分线BF交圆于点E，
∴利用角平分线的性质可得$\frac{AB}{BC}$=$\frac{AF}{CF}$，
∴$\frac{BC}{CF}$=$\frac{AB}{AF}$，
∴$\frac{AB}{AF}$=$\frac{AD}{AB}$，
∴AB²=AD×AF，
∵BD²=AD×DC，
∴$\frac{A{B}^{2}}{B{D}^{2}}$=$\frac{AF}{CD}$．

点评 本题考查圆的切线的性质，考查三角形相似性质的运用，考查学生分析解决问题的能力，属于中档题．