题目内容
已知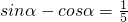 ,0≤x≤π,则tan2α=________.
,0≤x≤π,则tan2α=________.

分析:把所给的条件两边平方,写出正弦和余弦的积,判断出角在第一象限,求出两角和的结果,解方程组求出正弦和余弦值,进而得到正切值,用二倍角公式得到结果.
解答:∵
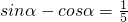 ,①0≤x≤π
,①0≤x≤π∴1-2sinαcosα=
 ,
,∴2sinαcosα=

∴

∴1+2sinαcosα=
 ,
,∴sinα+cosα=
 ,②
,②由①②得sinα=
 ,cosα=
,cosα= ,
,∴tanα=
 ,
,∴

故答案为:-

点评:本题考查三角函数同角的三角函数关系,解题的关键是分析角的范围,关键正弦值和余弦值的积,判断范围.

练习册系列答案
相关题目
已知f(x)=xlgx则f(x)( )
| A、在(0,e)上单调递增 | ||||
| B、在(0,10)上单调递增 | ||||
C、在(0,
| ||||
D、在(0,
|
已知函数f(x)=
,则y=f(x-1)+1的单调递减区间为( )
| 1 |
| x |
| A、[0,1) |
| B、(-∞,0) |
| C、{x|x≠1} |
| D、(-∞,1)和(1,+∞) |