函数f(x)=lnx-2x的单调递增区间为( )A．B．$$C．$$D．$$ 题目和参考答案——青夏教育精英家教网—

题目内容

5．函数f（x）=lnx-2x的单调递增区间为（　　）

A．

（-∞，2）

B．

$（-∞，\frac{1}{2}）$

C．

$（0，\frac{1}{2}）$

D．

$（\frac{1}{2}，+∞）$

分析求出原函数的导函数，由导函数大于0求解x的范围得答案．

解答解：由f（x）=lnx-2x，得
$f′（x）=\frac{1}{x}-2=\frac{1-2x}{x}$（x＞0）．
由f′（x）＞0，得$\frac{1-2x}{x}＞0$，得x$＜\frac{1}{2}$．
∴函数f（x）=lnx-2x的单调递增区间为（0，$\frac{1}{2}$）．
故选：C．

点评本题考查利用导数研究函数的单调性，明确导函数的符号与原函数单调性间的关系是关键，是基础题．

练习册系列答案

创新成功学习名校密卷系列答案

名师点拨课时作业甘肃教育出版社系列答案

16．若$\left\{\begin{array}{l}{sinθ＜0}\\{tanθ＞0}\end{array}\right.$ 则角θ所在的象限是（　　）

13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上三点A，B，P（位于x轴同侧）椭圆C的左、右焦点分别为F₁（-1，0），F₂（1，0），离心率为$\frac{\sqrt{2}}{2}$
（Ⅰ）当A的坐标为（0，1），AF₁∥BF₂时，求$\frac{|A{F}_{1}|}{|B{F}_{2}|}$的值
（Ⅱ）当直线AP经过点（-2，0），且BP⊥y轴时，判断直线AF₁与BF₂的位置关系，并说明理由．

20．某互联网理财平台为增加平台活跃度决定举行邀请好友拿奖励活动，规则是每邀请一位好友在该平台注册，并购买至少1万元的12月定期，邀请人可获得现金及红包奖励，现金奖励为被邀请人理财金额的1%，且每邀请一位最高现金奖励为300元，红包奖励为每邀请一位奖励50元．假设甲邀请到乙、丙两人，且乙、丙两人同意在该平台注册，并进行理财，乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如表：

理财金额	1万元	2万元	3万元
乙理财相应金额的概率	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$
丙理财相应金额的概率	$\frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{6}$

（1）求乙、丙理财金额之和不少于5万元的概率；
（2）若甲获得奖励为X元，求X的分布列与数学期望．

10．3名学生报名参加艺术体操、美术、计算机、航模四个课外兴趣小组，每人选报一种，则不同的报名种数有64．

17．在复平面中，下列复数中所对应的点在第三象限的是（　　）

14．式子$lg4+2lg5+{4^{-\frac{1}{2}}}$的化简结果为$\frac{5}{2}$．

15．

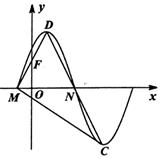如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象，M，N是它与x轴的两个交点，D，C分别为它的最高点和最低点，点F（0，1）是线段MD的中点，三角形MDC的面积为$\frac{2π}{3}$．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x）-m＞0在$x∈[{-\frac{π}{36}，\frac{π}{36}}]$上恒成立，求m的取值范围；
（Ⅲ）将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位，再往上平移1个单位，得到函数y=g（x）的图象．求y=g（x）在区间[2009π，2017π]上的零点个数．

试题分类