题目内容
已知数列{an}的前n项和Sn,且满足Sn=2an-2.(n∈N*)
(1)求数列{an}的通项an.
(2)若数列{bn}满足bn=log2an,Tn为数列{
}的前n项和,求证Tn≥
.
(1)求数列{an}的通项an.
(2)若数列{bn}满足bn=log2an,Tn为数列{
| bn |
| an |
| 1 |
| 2 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由于满足Sn=2an-2.(n∈N*),可得当n=1时,a1=2a1-2,解得a1;当n≥2时,an=Sn-Sn-1,化为an=2an-1,利用等比数列的定义与通项公式即可得出.
(2)bn=log2an=log22n=n.可得
=
.利用“错位相减法”即可得出.
(2)bn=log2an=log22n=n.可得
| bn |
| an |
| n |
| 2n |
解答:
(1)解:∵满足Sn=2an-2.(n∈N*),
∴当n=1时,a1=2a1-2,解得a1=2;
当n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2),化为an=2an-1,
∴数列{an}的通项an是等比数列,
∴an=2n.
(2)证明:bn=log2an=log22n=n.
∴
=
.
∴数列{
}的前n项和Tn=
+
+
+…+
,
∴
Tn=
+
+…+
+
,
∴
Tn=
+
+
+…+
-
=
-
=1-
-
,
∴Tn=2-
.
∵
>
,
∴Tn≥T1=
.
∴当n=1时,a1=2a1-2,解得a1=2;
当n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2),化为an=2an-1,
∴数列{an}的通项an是等比数列,
∴an=2n.
(2)证明:bn=log2an=log22n=n.
∴
| bn |
| an |
| n |
| 2n |
∴数列{
| bn |
| an |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n-1 |
| 2n |
| n |
| 2n+1 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-
| 2+n |
| 2n |
∵
| 2+n |
| 2n |
| 3+n |
| 2n+1 |
∴Tn≥T1=
| 1 |
| 2 |
点评:本题考查了比数列的通项公式与前n项和公式、“错位相减”、对数的运算性质、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
与命题“若p则q”的否命题真假相同的命题是( )
| A、若q 则p |
| B、若¬p则q |
| C、若¬q则p |
| D、若¬p则¬q |
若函数y=f(x)唯一的一个零点同时在区间(0,2),(1,2),(0,4),则下列命题中正确的是( )
| A、函数f(x)在区间(0,1)内有零点 |
| B、函数f(x)在区间(1,1.5)内有零点 |
| C、函数f(x)在区间(2,4)内无零点 |
| D、函数f(x)在区间(1,4)内无零点 |
函数y=Asin(ωx+φ)图象的一部分如图所示,则此函数的解析式可以写成( )
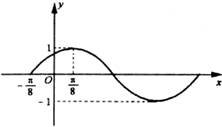

A、y=sin(2x+
| ||
B、y=sin(x+
| ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|