题目内容
函数y=x2+x(-1≤x≤3)的值域是( )
| A、[0,12] | ||
B、[
| ||
C、[
| ||
D、[
|
考点:函数的值域
专题:计算题,函数的性质及应用
分析:利用配方法求函数的值域.
解答:
解:y=x2+x=(x+
)2-
,
∵-1≤x≤3,
∴-
≤x2+x≤12,
故选B.
| 1 |
| 2 |
| 1 |
| 4 |
∵-1≤x≤3,
∴-
| 1 |
| 4 |
故选B.
点评:本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
相关题目
已知函数f(x)=-
sin(2x+
)+6sinxcosx-2cos2x+1.
(1)写出函数f(x)的最小正周期和对称轴方程;
(2)求f(x)在区间[0,
]的最值以及取得最值时的相应的x的值.
| 2 |
| π |
| 4 |
(1)写出函数f(x)的最小正周期和对称轴方程;
(2)求f(x)在区间[0,
| π |
| 2 |
阅读下列程序则该程序对应的程序框图(如图)中,①,②两个判断框内要填写的内容分别是( )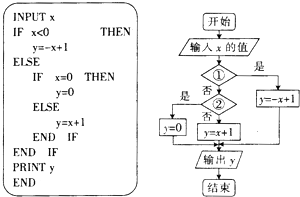

| A、x>0?x<0? |
| B、x>0?x=0 |
| C、x<0?x=0 |
| D、x≥0? x<0 |
五位同学参加某作家的签字售书活动,则甲、乙都排在丙前面的方法有( )
| A、20种 | B、24种 |
| C、40种 | D、56种 |
设a>1,定义f(n)=
+
+…+
,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7+7loga+1b恒成立,则实数b的取值范围是( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
A、(2,
| ||
| B、(0,1) | ||
| C、(0,4) | ||
| D、(1,+∞) |