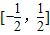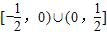题目内容
设z1是虚数,z2=z1+
是实数,且-1≤z2≤1
(1)求|z1|的值以及z1的实部的取值范围;
(2)若ω=
,求证:ω为纯虚数.
| 1 |
| z1 |
(1)求|z1|的值以及z1的实部的取值范围;
(2)若ω=
| 1-z1 |
| 1+z1 |
(1)设z1=a+bi(a,b∈R,且b≠0),
则z2=z1+
=a+bi+
=(a+
)+(b-
)i
∵z2是实数,b≠0,
∴有a2+b2=1,即|z1|=1,
∴可得z2=2a,
由-1≤z2≤1,得-1≤2a≤1,
解得-
≤a≤
,
即z1的实部的取值范围是[-
,
].
(2)ω=
=
=
=-
i
∵a∈[-
,
],b≠0,
∴ω为纯虚数.
则z2=z1+
| 1 |
| z1 |
| 1 |
| a+bi |
| a |
| a2+b2 |
| b |
| a2+b2 |
∵z2是实数,b≠0,
∴有a2+b2=1,即|z1|=1,
∴可得z2=2a,
由-1≤z2≤1,得-1≤2a≤1,
解得-
| 1 |
| 2 |
| 1 |
| 2 |
即z1的实部的取值范围是[-
| 1 |
| 2 |
| 1 |
| 2 |
(2)ω=
| 1-z1 |
| 1+z1 |
| 1-a-bi |
| 1+a+bi |
| 1-a2-b2-2bi |
| (1+a)2+b2 |
| b |
| a+1 |
∵a∈[-
| 1 |
| 2 |
| 1 |
| 2 |
∴ω为纯虚数.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
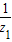 是实数,且-1≤z2≤1,则z1的实部取值范围是( )
是实数,且-1≤z2≤1,则z1的实部取值范围是( )