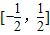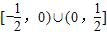题目内容
设z1是虚数,z2=z1+
是实数,且-1≤z2≤1,则z1的实部取值范围是( )
| 1 |
| z1 |
分析:设z1=a+bi,b≠0,则由z2=z1+
是实数,可得b-
=0,求得 a2+b2=1,故z2=a+
=2a.再由-1≤z2≤1,可得-1≤2a≤1,由此解得a的范围
| 1 |
| z1 |
| b |
| a2+b2 |
| a |
| a2+b2 |
解答:解:设z1=a+bi,b≠0,则由z2=z1+
=a+bi+
=a+bi+
是实数,
∴b-
=0,∴a2+b2=1,故z2=a+
=2a.
再由-1≤z2≤1,可得-1≤2a≤1,解得-
≤a≤
,
故选B.
| 1 |
| z1 |
| 1 |
| a+bi |
| a-bi |
| a2+b2 |
∴b-
| b |
| a2+b2 |
| a |
| a2+b2 |
再由-1≤z2≤1,可得-1≤2a≤1,解得-
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
相关题目
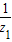 是实数,且-1≤z2≤1,则z1的实部取值范围是( )
是实数,且-1≤z2≤1,则z1的实部取值范围是( )