题目内容
F1，F2是椭圆
+
=1的两个焦点，点P是椭圆上任意一点，从F1引∠F1PF2的外角平分线的垂线，交F2P的延长线于M，则点M的轨迹是________．
以点F2为圆心，半径为2a的圆
分析：根据等腰三角形“三线合一”，得到|MP|=|F1P|，从而|PF1|+|PF2|=|MF2|，结合椭圆的定义可得|MF2|=2a，即动点M到点
F2的距离为定值2a，由此即可得到动点M的轨迹对应的图形．
解答：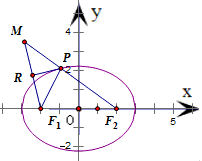
解：设从F1引∠F1PF2的外角平分线的垂线，垂足为R
∵△PF1M中，PR⊥F1M且PR是∠F1PM的平分线
∴|MP|=|F1P|，可得|PF1|+|PF2|=|PM|+|PF2|=|MF2|
根据椭圆的定义，可得|PF1|+|PF2|=2a，
∴|MF2|=2a，即动点M到点F2的距离为定值2a，
因此，点M的轨迹是以点F2为圆心，半径为2a的圆．
故答案为：以点F2为圆心，半径为2a的圆．
点评：本题给出椭圆上动点P，求点M的轨迹方程，着重考查了椭圆的定义和简单几何性质，以及等腰三角形“三线合一”等知识，属于中档题．
分析：根据等腰三角形“三线合一”，得到|MP|=|F1P|，从而|PF1|+|PF2|=|MF2|，结合椭圆的定义可得|MF2|=2a，即动点M到点
F2的距离为定值2a，由此即可得到动点M的轨迹对应的图形．
解答：
解：设从F1引∠F1PF2的外角平分线的垂线，垂足为R∵△PF1M中，PR⊥F1M且PR是∠F1PM的平分线
∴|MP|=|F1P|，可得|PF1|+|PF2|=|PM|+|PF2|=|MF2|
根据椭圆的定义，可得|PF1|+|PF2|=2a，
∴|MF2|=2a，即动点M到点F2的距离为定值2a，
因此，点M的轨迹是以点F2为圆心，半径为2a的圆．
故答案为：以点F2为圆心，半径为2a的圆．
点评：本题给出椭圆上动点P，求点M的轨迹方程，着重考查了椭圆的定义和简单几何性质，以及等腰三角形“三线合一”等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知：F1，F2是椭圆