题目内容
已知长轴在x轴上的椭圆的离心率e=
,且过点(1,
).
(1)求椭圆的标准方程;
(2)若P是椭圆上任意一点,F1、F2是椭圆的左、右焦点,求PF1•PF2的最大值.
| 1 |
| 2 |
| 3 |
| 2 |
(1)求椭圆的标准方程;
(2)若P是椭圆上任意一点,F1、F2是椭圆的左、右焦点,求PF1•PF2的最大值.
分析:(1)设椭圆的方程为
+
=1,由已知中椭圆的离心率和所过定点,可构造关于a,b的方程组,解方程组求出a,b的值,可得椭圆的标准方程;
(2)由(1)可求出椭圆的左、右焦点坐标,进而根据三角形两边之和大于第三边和基本不等式,可得PF1•PF2的最大值
| x2 |
| a2 |
| y2 |
| b2 |
(2)由(1)可求出椭圆的左、右焦点坐标,进而根据三角形两边之和大于第三边和基本不等式,可得PF1•PF2的最大值
解答:解:(1)由题意,可设椭圆的方程为
+
=1(a>b>0).
因为e=
,
所以
=
=
,
即
=
.…(4分)
又由椭圆过点(1,
)得:
+
=1,即
+
=1.
解得a2=4,b2=3,
所以椭圆的方程为
+
=1.…(8分)
(2)由(1)得F1(-1,0),F2(1,0).
因为PF1+PF2=2a=4,…(10分)
所以PF1•PF2≤(
)2=4,当且仅当PF1=PF2=2时等号成立,
所以(PF1•PF2)max=4.…(15分)
| x2 |
| a2 |
| y2 |
| b2 |
因为e=
| 1 |
| 2 |
所以
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 1 |
| 4 |
即
| b2 |
| a2 |
| 3 |
| 4 |
又由椭圆过点(1,
| 3 |
| 2 |
| 1 |
| a2 |
(
| ||
| a2 |
| 1 |
| a2 |
| 9 |
| 4b2 |
解得a2=4,b2=3,
所以椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由(1)得F1(-1,0),F2(1,0).
因为PF1+PF2=2a=4,…(10分)
所以PF1•PF2≤(
| PF1+PF2 |
| 2 |
所以(PF1•PF2)max=4.…(15分)
点评:本题考查的知识点是椭圆的标准方程,基本不等式,椭圆的简单性质,难度不大,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目


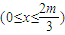 和椭圆弧
和椭圆弧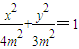

 和椭圆弧
和椭圆弧
