题目内容
设实数x,y满足条件
若目标函数z=ax+by(a>0,b>0)的最大值为12,则
+
的最小值为 .
|
| 2 |
| a |
| 3 |
| b |
考点:简单线性规划
专题:
分析:由约束条件作出可行域,求出最优解,把最优解的坐标代入目标函数得到
+
=1,然后利用基本不等式求最值.
| a |
| 3 |
| b |
| 2 |
解答:
解:由约束条件
作出可行域如图,
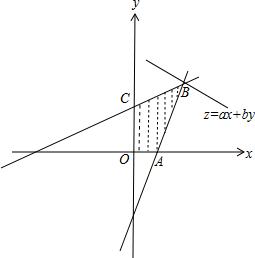
联立
,解得B(4,6),
化目标函数z=ax+by为y=-
x+
,
由图可知,当直线y=-
x+
过B时z有最大值,
为4a+6b=12,即
+
=1,
则
+
=(
+
)(
+
)=
+
+
+
≥
+2
=
.
当且仅当
,即a=b=
时上式等号成立.
故答案为:
.
|

联立
|
化目标函数z=ax+by为y=-
| a |
| b |
| z |
| b |
由图可知,当直线y=-
| a |
| b |
| z |
| b |
为4a+6b=12,即
| a |
| 3 |
| b |
| 2 |
则
| 2 |
| a |
| 3 |
| b |
| 2 |
| a |
| 3 |
| b |
| a |
| 3 |
| b |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| b |
| a |
| a |
| b |
| 13 |
| 6 |
|
| 25 |
| 6 |
当且仅当
|
| 6 |
| 5 |
故答案为:
| 25 |
| 6 |
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若不等式
≤a≤
在t∈[1,4]上恒成立,则a的取值范围是( )
| t |
| t2+9 |
| t+2 |
| t2 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知0<x<1,则x(3-3x)取最大值时x的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
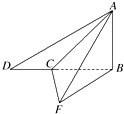 如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(
如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(