题目内容
19.已知等差数列的{an}前n项和为Sn,且S3-2a2=3,S4=16;数列{bn}满足b1+2b2+3b3+…+nbn=(n-1)2n+1.(1)求数列{an},{bn}的通项公式;
(2)记cn=an+(-1)nlog2bn,数列{cn}的前n项和为Tn(n∈N*),当n为奇数时,求Tn的表达式.
分析 (1)设等差数列的{an}的公差为d,由S3-2a2=3,S4=16,利用等差数列的通项公式及其前n项和公式即可得出.由数列{bn}满足b1+2b2+3b3+…+nbn=(n-1)2n+1,利用递推关系即可得出.
(2)cn=an+(-1)nlog2bn=(2n-1)+(-1)n(n-1),利用等差数列的前n项和公式分组求和即可得出.
解答 解:(1)设等差数列的{an}的公差为d,∵S3-2a2=3,S4=16,
∴$3{a}_{1}+\frac{3×2}{2}$d-2(a1+d)=3,$4{a}_{1}+\frac{4×3}{2}d$=16,
解得a1=1,d=2.
∴an=1+2(n-1)=2n-1.
∵数列{bn}满足b1+2b2+3b3+…+nbn=(n-1)2n+1,
∴b1=1;n≥2时,b1+2b2+3b3+…+(n-1)bn-1=(n-2)2n-1+1,
∴nbn=n•2n-1,可得bn=2n-1(n=1时也成立).
∴bn=2n-1.
(2)cn=an+(-1)nlog2bn=(2n-1)+(-1)n(n-1),
数列{cn}的前n项和为Tn(n∈N*),当n为奇数时,
Tn=[1+3+…+(2n-1)]+[0+1-2+…-(n-1)]
=$\frac{n×(1+2n-1)}{2}$-$\frac{n-1}{2}$=n2-$\frac{n}{2}$$+\frac{1}{2}$.
点评 本题考查了递推关系、等差数列的通项公式及其前n项和公式、分组求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知实数x,y满足$\left\{\begin{array}{l}{2x+y≥4}\\{4x-y≤8}\\{x-y≥-1}\end{array}\right.$,则x2+y2-2x的取值范围是( )
| A. | [-$\frac{1}{5}$,19] | B. | [-$\frac{1}{5}$,+∞) | C. | [3,19] | D. | [-$\frac{1}{5}$,3] |
14.设全集U=R,集合A={x|x>0},B={x|x<1},则集合(∁UA)∩B=( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (1,+∞) | D. | [1,+∞) |
4.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
①若m⊥α,α⊥β,则m∥β
②若m⊥α,α∥β,n?β,则m⊥n
③若m?α,n?β,m∥n,则α∥β
④若n⊥α,n⊥β,m⊥β,则m⊥α
①若m⊥α,α⊥β,则m∥β
②若m⊥α,α∥β,n?β,则m⊥n
③若m?α,n?β,m∥n,则α∥β
④若n⊥α,n⊥β,m⊥β,则m⊥α
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
9.已知a,b,c∈R+,且ab+bc+ca=1,那么下列不等式中正确的是( )
| A. | a2+b2+c2≥2 | B. | (a+b+c)2≥3 | C. | $\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥2$\sqrt{3}$ | D. | abc(a+b+c)≥$\frac{1}{3}$ |
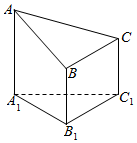 如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体,截面为△ABC,已知AA1=4,BB1=2,CC1=3,在边AB上是否存在一点O,使得OC∥平面A1B1C1?
如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体,截面为△ABC,已知AA1=4,BB1=2,CC1=3,在边AB上是否存在一点O,使得OC∥平面A1B1C1?