题目内容
6.已知复数z1=3-2i,z2=-2+3i.(1)求z1z2;
(2)若复数z满足$\frac{1}{z}=\frac{1}{z_1}+\frac{1}{z_2}$,求|z|.
分析 (1)根据复数的乘法即可求出,
(2)根据复数的混合运算即可求出z,再求出其模即可/
解答 解:(1)∵z1=3-2i,z2=-2+3i,
∴z1•z2=(3-2i)(-2+3i)=-6-6i2+9i+4i=13i;
(2)$\frac{1}{z}=\frac{1}{z_1}+\frac{1}{z_2}$=$\frac{{z}_{1}+{z}_{2}}{{z}_{1}•{z}_{2}}$=$\frac{1+i}{13i}$,
∴z=$\frac{13i}{1+i}$=$\frac{13i(1-i)}{(1+i)(1-i)}$=$\frac{-13+13i}{2}$=$\frac{13}{2}$+$\frac{13}{2}$i,
∴|z|=$\sqrt{\frac{169}{4}×2}$=$\frac{13\sqrt{2}}{2}$
点评 本题考查了复数的混合运算和复数的模,属于基础题.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 函数的极大值就是函数的最大值 | |
| B. | 函数的极小值就是函数的最小值 | |
| C. | 函数的最值一定是极值 | |
| D. | 闭区间上的连续函数一定存在最大值与最小值 |
18.已知函数f(x)=$\frac{1}{2}$ax2+bx+1,其中a∈{2,4},b∈{1,3},从f(x)中随机抽取1个,则它在(-∞,-1]上是减函数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | 0 |
15.已知正方体的外接球的体积为$\frac{32}{3}π$,则该正方体的表面积为( )
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{64}{3}$ | D. | 32 |
1.对任意的x,y∈(0,+∞),不等式ex+y-4+ex-y+4+6≥4xlna恒成立,则正实数a的最大值是( )
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}e$ | C. | e | D. | 2e |
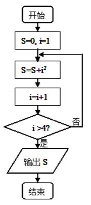
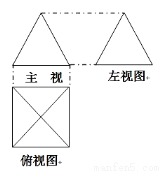
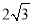 cm
cm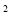 B.
B.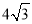 cm2
cm2